Earth Science Today Lab, Distance to Stars (35-70 minutes, depending on math familiarity)

Part 1: Triangulation method
Distance to nearby stars is determined by triangulation.  The concept of triangulation is fairly straightforward:  you need to imagine a right triangle where one side of the triangle is the distance you want to measure (recall the measurement-of-a-tree exercise).  If you can measure one angle of the triangle other than the right angle (either one works) and the length of one other side of the triangle, then the side of interest can be calculated by geometric or trigonometric methods.
     Here is an exercise to practice "finding" triangles before we try to do stars.  Determine the length of one of the lab tables without actually measuring its length.
     You can use a protractor and a ruler (you can measure the width of the table or distance to the table, but you can't use the ruler to measure the length of the table).
     You can put some object on the far end of the table (rock, pencil) to triangulate against (that is, measure an angle toward).
You can do this by either using similar triangles or trigonometry. 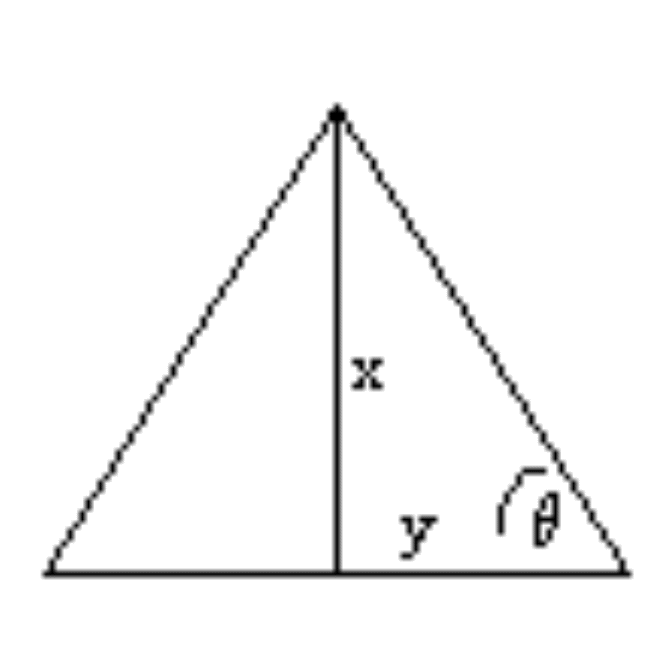You can use similar triangles drawn with a protractor if you want (measuring the length of the sides, which will be proportional to the sides on your "table" triangle), or the trigonometric equation given below.
Tanq = x/y   or x = y· (tanq ).

Length of Table (in inches): ____________________
_____________________________________________________________________________________________________________________
Part 2: Actual star distance
The concept of parallax is one we are all familiar with.  Hold your thumb out at arms length and close first one eye and then the other.  Notice the shift against the more distant background?  This is parallax.  Now bring your thumb toward you half-way and do the same thing.  Notice that the shift appears to be greater?  The difference in shift provides a means to measure the distance to your thumb (or to stars).  But first you need to find an imaginary triangle that will work, measure an angle, and measure one side of the triangle.  In measuring the distance to stars, one side of the triangle is taken as the distance from the Earth to the Sun (a value which we know).  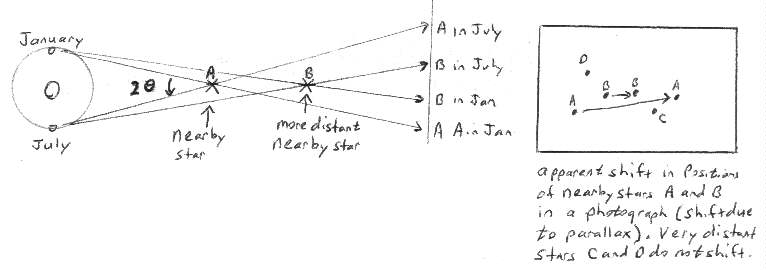The angle is measured by observing the parallax, which is how far the star appears to shift against the background of stars as the Earth orbits the Sun (analogous to closing one eye then the other).  Illustration of Parallax (unknown source).

The two images below are taken 6 months apart (thus the Earth has moved from one side of the Sun to the other side, a distance of about 2AU).  The star HT Cas is the closest to Earth of the stars in this image.  The angle between the two stars closest to HT Cas (other than HT Cas itself) is 0.000002778 degrees. This value is the "scale" by which you can determine other angles.
 
Step 1) figure out which star is HT Cas (hint: which one appears to have moved?)

Step 2) determine the angle that HT Cas has shifted due to Earth's change in position over 6 months time.
Hint: The angle that is important in these figures is the angle between two imaginary lines drawn between you (on Earth) and each position of the star. Thus, the angle you are interested in is not in the plane of the picture!  However, this angle is proportional to the distances between stars as seen in the image of the stars above. Therefore, you can figure out the angles by measuring distances between stars on the image (with a ruler).

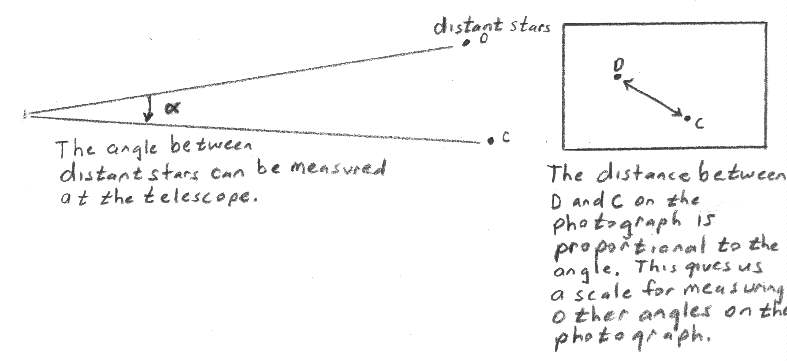
Measurement of the angle is accomplished by observing the distance of the apparent shift in the star on photographs taken 6 months apart.  This shift is proportional to the angle, with more distant stars having smaller angles and smaller distances of shift.

The distance can be converted to an angle by using the known angle between two other stars that do not shift position.  In this puzzle, the known angle is between two stars nearest to HTCas and is 0.000002778 degrees.

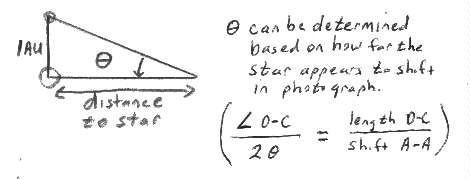
Finally, we can calculate the angle of shift of HTCas by comparing with the known angle between the nearby stars.  (The angle between the two nearby stars/the angle of shift in HTCas = the distance between the two nearby stars on the photo/the distance of shift in HTCas).
Composite illustration of measurement method

Step 3) Calculate the distance to HT Cas.
This can be accomplished by imagining a right triangle between the Earth, Sun, and HTCas.  The angle of this right triangle = 1/2 the angle between HT Cas original position and its new position.  We now know a length of one side of the triangle (=1AU the distance from Earth to the Sun) and one angle (theta = 1/2 the parallax angle).  We can therefore calculate the length of the other side of the triangle, which is the distance to the star.   One relationship that helps with this calculation is the following:  tan(angle theta) = ½diameter of Earth orbit/distance to the star).

Star's distance in AU _______________________________________

An example Triangulation activity appropriate for Junior High Students
Home Page (est.htm)     Previous Page (est3a.html)