Mineralogy: Substitution Rules

Earth Science Extras

by Russ Colson

Introduction

One of the fundamental parts of the definition of a mineral is that it has a crystal structure,that is, a lattice with a regular arrangement of atoms, meaning regular and somewhat fixed structural sites that contain cations (and anions). Another part of the definition of a mineral is that it has a 'definite' composition. For example, in the mineral halite, there is one sodium cation for each chlorine anion, NaCl,--you can't just willy-nilly have any particular proportion of those ions, thus the composition is definite. Notice, that 'definite' does not mean quite the same thing as 'fixed'. Sometimes other cations, like potassium (K), can replace some of the sodium (Na), forming a solid solution in the halite. However, the proportions of cations to anions is still fixed and the 'spots' or 'sites' where the cations and anions go maintains a similar structure, such that we might write the formula for the mineral as (Na,K)Cl, reflecting the solid solution between Na and K in the structure.

But what are the 'rules' that govern whether two ions can substitute for each other in a particular crystal structure?

Goldschmidt's Rules (simplified) are that two ions can substitute for each other in a crystal lattice if they are of similar size and charge (his guidelines suggested cations must be within ±15% in size, and within ±1 in charge). As an illustration of the concepts of substitutution and solid solution, we are going to examine substitutions in three different mineral structures: garnet, pyroxene, and feldspar.

Note: in preparation for this lesson, you might review concepts of bonding and coordination number, either online, or with the previous lesson "Mineralogy-Basics_Review-Atoms-and-Bonds"

Simple Substitutions in Garnet, Pyroxene, and Feldspar

Garnet:

Garnet is a nesosilicate, meaning that each tetrahedral cation (usually Si) is bonded to four oxygen anions, none of which are bonded to another tetrahedron--sometimes we say that none of the oxygens are bridging oxygens, meaning that none of the oxygens bridge between two tetrahedrons (usually meaning they don't bridge between silicon atoms). This means that the ratio of silicon to oxygen will be 1:4. This compares to a tectosilicate (sometimes called framework silicate) like quartz in which each oxygen is shared between two silicons (as we discussed when we considered the covalent bonding in quartz), in which the silicon to oxygen ratio is 1:2. In other words, in tectosilicates, all oxygens are bridging oxygens. Remembering that oxygen likes to share two outer shell electrons so as to gain a net of 8 in its outer shell, we see that, for the nesosilicates, something other than silicon must be providing for that balance. In garnet, the extra electrons to complete the oxygen outer shell come from cations in two different crystal sites called the "X" and "Y" sites in the garnet. This gives us the general formula for garnet of

X₃Y₂(TO₄)₃. Since the Tetrahedral site (T) is usually occupied by Si we can also give the formula as X₃Y₂(SiO₄)₃

Each formula unit of garnet contains three sets of SiO₄ tetrahedrons. The T tetrahedral 'T" sites have coordination numbers of 4, with 4 oxygen nearest neighbors, and thus only accommodating fairly small cations, like Si. Each formula unit also contains 3 "X" and 2 "Y" cations. In garnet, the "X" sites are spots that have a coordination number of 8 with surrounding oxygens, and so accommodate fairly large cations. The valence (charge) on this site is typically "+2", thus it accommodates larger divalent cations. The "Y" sites are spots with a coordination number of 6 with surrounding oxygens and typically have a valence (charge) of "+3" and so accommodate smaller trivalent cations.

An illustration of the these garnet cation sites is provided below. (Image comes from "Examination of the site preference in garnet type (X₃A₂B₃O₁₂; X=Y, A/B= Al, Ga, Fe) materials" by Rahin Sifat and Andrew P. Grosvenor, Solid State Sciences 83 (2018) 56–64.)

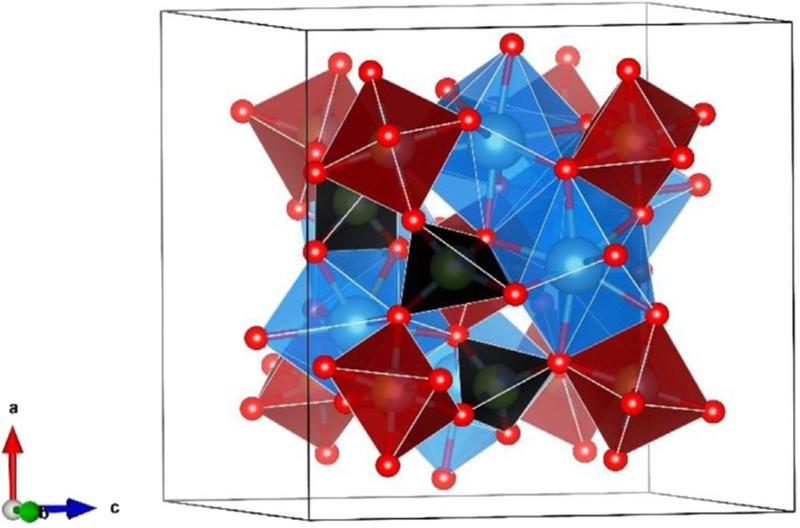
One example garnet mineral is Grossular, with a formula of Ca₃Al₂(SiO₄)₃. Ca²⁺ is of appropriate size for the 8-coordinated X site. Al³⁺ is of appropriate size for the 6-coordinated Y site. Also notice that this mineral is charge balanced, that is, its net charge, when all cations and anions are added up, is zero (a condition for stability of minerals). The charge balance can be established by adding up the charges: Ca has a valence of +2, Al a valence of +3, and Si a valence of +4 (even though some of these cations bond primarily by covalent bonds, it is still useful to think of a cationic charge for the exercises we do here and below). O has a valence of -2. Thus, 3*2 + 2*3 + 3*4 = +24, and 12 * (-2) = -24, providing for charge balance.

What other compositions might be reasonable for garnet, with the constraint of maintaining charge balance in the crystal (total charge of cations equals the total charge of anions) and substituting cations on the crystal sites of 'similar size and charge?'

In answering this question, you might consider the graph below that shows the ionic sizes of a variety of cations ratioed to an oxygen anion size of 1.32 Angstroms. The graph shows the approximate 'cut off' values for different coordination numbers (CN). Valence is shown on the X axis (some cations can exist in more than one valence state, as shown). Also, there is some variation in ionic size depending on the size of the site that is occupied. For example, Na is fairly comressible (squishy), and will be smaller if squeezed into a lower coordination number site than if it is in a larger coordination number site. This is shown by the multiple values for individual elements with the same valence. (Data are from Zoltai and Stout 1984, as slightly modified in https://opengeology.org/Mineralogy/13-crystal-structures/ with some approximations based on the different set of ionic radii from Shannon and Prewitt, 1969 and Shannon, 1976.)

 

Pyroxene:

Pyroxene is a single chain silicate (inosilicate), meaning that tetrahedra are connected to other tetrahedra in long chains. In this configuration, the ratio of tetrahedral sites (usualy filled by Si) to oxygen is 1:3. The structural formula for the mineral pyroxene is

M2M1T₂O₆, or putting common Si into the tetrahedral site, M2M1Si₂O₆

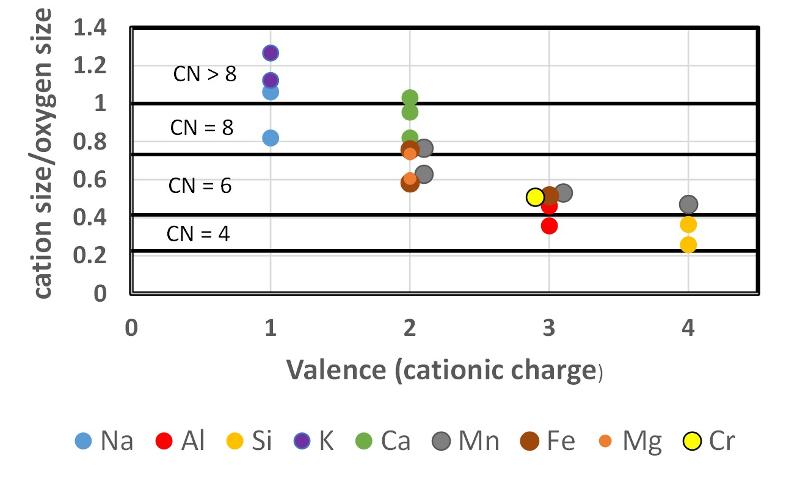
The two M sites are cation sites. Consider the diagram below for one type of pyroxene mineral (Ca-rich pyroxene) from "Structural and chemical variations in pyroxenes" by Maryellen Cameron and J. J. Papike, American Mineralogist, Volume 66, pages I-50, 1981 (projected onto the 100 plane).

So, in pyroxene, M1 is a 6-coordinated octahedral site. however, although shown as 8-coordinated in the figure above, M2 is a more complex 'stretchy" site that can be either octahedral or 8-coordinated, although not usally a combination of both, meaning that it can hold the bigger cations, or the smaller 6-coordinated cations, but not an easy mixture of both. The larger 8-coordination of the M2 site results in distortions in the crystal structure that reduce the symmetry, so that many of the pyroxenes with 6-coordinated M2 sites are in the orthorhombic system whereas the 8-coordinated M2 site pyroxenes are often monoclinic.

The cation size-charge-coordination chart from above is reproduced here for convenience.

 

Feldspars

Feldspars are tectosilicates (or framework silicates), meaning that each tetrahedron shares all four corners with other tetrahedrons (or, said another way, each tetrahedral cation shares all of its oxygens with other tetrahedral cations, such that all of the oxygens are bridging oxygens). In tectosilicates, since every oxygen is shared between two tetrahedra the ratio of tetrahedral cations to oxygen is 1:2 (like in quartz). In feldspar, the clusters of tetrahedra are arranged so as to make big 'holes' in the structure that are occupied by large cations, like K. The structure for feldspar below comes from "Polymorphism of Feldspars above 10GPa," by Pakkhomova et al, 202, Nature Communications, https://doi.org/10.1038/s41467-020-16547-4.

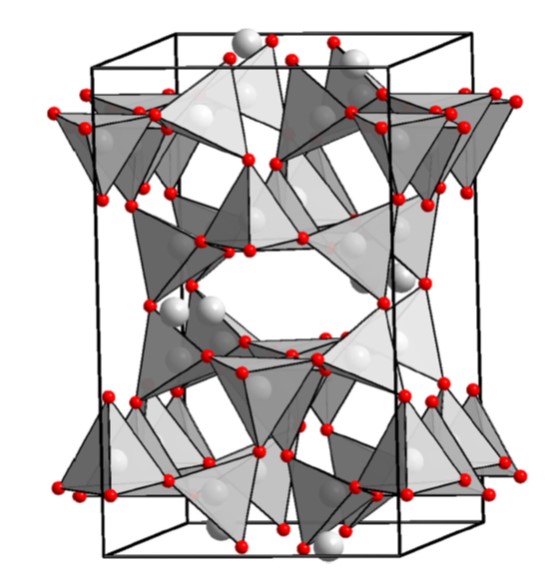
The structural formula for feldspar is

AT₄O₈,

where A is a large, high coordination-number site (often 7-9), and T is a tetrahedral site. The A site, although sometimes of coordination of only 7, is generally quite large and only suited to larger cations that are marked as CN>8 in the chart above.

An example feldspar mineral is Orthoclase: K(AlSi₃)O₈, where the elements in parentheses are those in tetrahedral sites and K is in the high-coordination "A" site.

 

Charge Balancing Coupled Substitution Mechanisms in Feldspar and Pyroxene

Consider that Ca is also a major element in feldspar, occupyiing the large A site. What has to happen for Ca to substitute for the K or Na in the feldspar structure?

Na(AlSi₃)O₈ >>>> Ca(AlSi₃)O₈ ?????

The problem with simply replacing the Na (with a valence of +1) with Ca (with a valence of +2) is that we have a charge imbalance. But what if at the same time we substitute Na for Ca, we also substitute another of the tetrahedral Si cations (+4) with an Al (+3). That gets our charge back in balance.

Ca(Al₂Si₂)O₈

This is the formula for Anorthite. Albite [Na(AlSi₃)O₈] and Anorthite form a complete solid-solutions series with Ca+Al substituting for Na+Si, with all intermediate compositions possible.

Similar coupled substitutions are possible in Pyroxene. Using the size-charge-coordination chart above (and reproduced below), and remenbering the formula for pyroxene (M2M1T₂O₆, and remembering the need for minerals to maintain a neutral charge, try to predict which formulae are reasonable pyroxenes. Remember that in pyroxene the M1 site is octahedral (6-coordinated) and the M2 site can be either 6- or 8-coordinated.

 

Applying Substitution Rules to Trace Element Partitioning

Introduction to how substitution rules affect partitioning:

Trace element partitioning refers to how elements that exist at low concentrations in nature, basically cation-forming elements that are not Si, Al, Ca, Mg, Fe, Na, K, and Mn, partition between different phases that are in contact with each other and approaching equilibrium. For example, we might be interested in how Ni, Sr, or Rare Earth Elements (REE) are distributed between solid phases like pyroxene, feldspar, or garnet and another phase such as silicate melt (magma).

We are not going to consider all of the factors involved in partition coefficient reactions (which, like any chemical reaction, include temperature, pressure, and the chemical activities of the partitioning elements, including charge-balancing ions), but one constraint of the reaction is how well-suited a particular trace cation is to the crystal lattice site into which it is substituting (and also how well-suited any charge balancing coupled substitution is to its site). Ref: Colson et al, Temperature and composition dependencies of trace element partitioning: Olivine/melt and low-Ca pyroxene melt, GCA 52, 1988,

For trace elements, it is often helpful to consider that any particular crystal site has an 'optimum' cation size that fits into it, where a large cation stretches the site outwards, increasing its energy (a less favorable state), and a smaller cation causes the anions to have to compress inwards more, again increasing energy. For our considerations below, we will compare the trace cation size to the size of an approximate "optimum" cation size.

Let's consider a couple of simple examples of how this might apply to trace element partitioning.

First some language:

A "partition coefficient" might be defined as the concentration of a particular chemical component in a crystalline phase (usually an element) divided by the concentrationof that same component in the melt phase with which the crystal is in equilibrium. If the partition coefficient is >1, then we say that the element is compatible in that crystal phase. If the partition coefficient is < 1, then we say that the element is incompatible in that phase.

Compatibility or incompatibility depends on many factors, including the suitability of a cation for a particular site in a crystal (based on its size), composition of the crystal and melt phases, temperature, pressure, and the availabilty and suitability of other elements to charge balance the crystal. In the exercises below, we are going to mainly focus on the the suitability of a cation to 'fit' into a particular mineral and not worry about charge balancing and other constraints. Thus, I will use "suitable or unsuitable" rather than "compatible or incompatible", although these will be related to each other. In general, cations that 'fit' well into a particular crystal site (that is, are suitable) but require a coupled substitution for charge balancing, will have a lower partitition coefficient than expected solely on the basis of cation "fit" into the site, and may be incompatible even though of suitable size.

Goldschmit's Rules, in their more complete form, took into account some aspects of an 'optimum' cation size--a substitution on a crystal site is most suitable if the size of the substituting cation is within 15% of the value of the major cation. Using Goldschidt's "within 15%" as our guide, we will declare that any cation within 15% of the "optimum" size for a particular site is "suitable" for that site. Greater deviation from the 'optimum' size will result in a higher energy state, and thus a lower concentration for that cation in the site. Increasing unsuitability results in increasingly low partition coefficients.

Partitioning Substitution on 6-coordinated sites: Olivine

The M1 and M2 sites in olivine (M2M1TO₄) are 6-coordinated sites. The "optimum" cation size for the M1 and M2 sites in olivine depends on the composiiton of the olivine, temperature, and pressure, and also on the charge of the cations in the M sites, but at low pressure we can infer a "typical" optimum--for the purposes of the exercises below--of perhaps about 0.71. Ref: Shea et al 2019: Phosphorus and aluminum zoning in olivine: contrasting behavior of two nominally incompatible trace elements, Contributions to Mineralogy and Petrology 174(85).

Below is a list of cation sizes for cations occupying octahedral (6-coordinated) sites (data in this case come from Shannon and Prewitt (1969) Acta Crystallographica, p25-946, and Shannon (1976) Acta Crystallographica 751-767. For your convenience in addressing the ensuing questions, the list has been sorted by cation size.

 

Partitioning Substitution on 8-coordinated sites: Garnet

We are only considering the X site in garnet for this exercise. An approximate "optimum" size for the 8-coordinated X site in a pyrope (Mg on X site) and almandine (Fe²⁺ on the X site) rich garnet (ignoring the effects of varying mineral composition) is 0.93 Angstroms (Sun and Liang, "The importance of crystal chemistry on REE partitioning between mantle minerals (garnet, clinopyroxene, orthopyroxene, and olivine) and basaltic melts," Chemical Geology 358 (2013) 23–36).

Below is a list of cation sizes for cations occupying 8-coordinated sites (data again come from Shannon and Prewitt (1969) Acta Crystallographica, p25-946, and Shannnon (1976) Acta Crystallographica 751-767. For your convenience in addressing the ensuing questions, the list has been sorted by cation size.)

 

Partitioning Substitution on 8-coordinated sites: Ca-Pyroxene

The M2 site in Ca-pyroxene is 8-coordinated with an optimum of around 1.05 Angstroms.

 

Partitioning Substitution on 7-9-coordinated sites: Feldspar

We are going to consider plagioclase feldspar, that is feldspar in the solid solution series from CaAl₂Si₂O₈ to NaAlSi₃O₈. The approximate 'optimum' size for the large "A" site in the feldspar is 1.2 Angstroms (ignoring variability with cation charge and plagioclase composition).

Below is the same list of cation sizes for cations occupying 8-coordinated sites as given above (data from Shannon and Prewitt (1969) Acta Crystallographica, p25-946, and Shannnon (1976) Acta Crystallographica 751-767. For your convenience in addressing the ensuing questions, the list has been sorted by cation size.)

Because of their very similar chemical properties, the Rare Earth Elements (REE) are often a sensitive indicator of subtle differences between environments in which various crystals might form. The atomic number of the REE increases incrementally from 57 for La (on the light REE side), to 62 for Sm, 63 for Eu, and 72 and 73 for Yb and Lu on the heavy REE side. To see the effect of subtly differing properties in igneous rocks or minerals, we often plot the concentrations of all of the REE in order of increasing mass (normalized to a standard such as chondritic meteorites). Because chemical properties are mostly the same, but the cation size decreases as atomic number increases, the REE often trend one way or the other after a magmatic or hydrothermal process has affected them. However, one REE, Eu, can be chemically different and stand out in what is often called a Europium Anomaly. This is because, although the other REE are usually trivalent, Eu can be divalent at sufficiently low oxygen activities. This affects both valence (affecting charge balance) and cation size.

 

Interesting Note: The discovery of what appeared to be a strong negative Eu anomaly at depth in the Moon, and a strong positive Eu anomaly in the plagioclase-rich highlands crust of the Moon, shortly after the first Apollo samples were brought back from the Moon, became part of the argument that the Moon once had a magma ocean that crystallized, with plagioclase "rock bergs" floating to the surface to become the plagioclase-rich highlands crust.

  

 last updated 10/24/2022.   Text and pictures are the property of Russ Colson, except as noted.