Mineralogy Basics Review: Atoms and Bonds

Earth Science Extras

by Russ Colson

Ball-and-Stick model of a sheet silicate with atoms represented by colored balls and bonds represented by metal sticks. This model is for illite, which is a general name for a group of non-expanding clay minerals. This structure is very similar to the mica mineral muscovite.

Atoms:

Below is a very terse review of atoms. Ideally, you should do some reading online to expand your understanding of atoms further, perhaps expanding your understanding into models for the atom that are more sophisticated than the simple introductory model provided here..

A simplistic model for the atom includes a central nucleus--which contains protons (particles with a charge of +1) and neutrons (particles of similar mass to protons but with no charge)--surrounded by a cloud of electrons (particles with a mass insignficantly small compared to the proton and neutron and with a charge of -1). A simple model of an atom (of Lithium) is shown below.

If the number of protons and electrons are equal, then the atom itself will be neutral. However, if there is a mismatch between the numbers of electrons and neutrons, then the atom will have an electrical charge and we will call it an ion. Often, atoms with positive charges we call cations and those with negative charges we call anions. An example of a Lithium ion (a cation) is shown below.

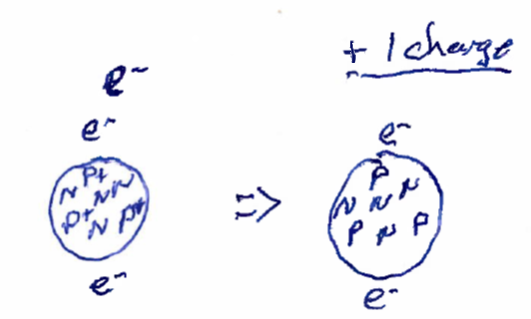
The number of protons in an atom, which we refer to as the atomic number, defines what element that the atom is. So, for example, if an atom has 3 protons in the nucleus, that atom is always Lithium regardless of the number of electrons. Thus, both of the illustrations above are Lithium, one being a neutral atom and the other being a Lithium cation.

Atoms can also have different numbers of neutrons, regardless of the number of protons and electrons. Two atoms with the same number of protons but different numbers of neutrons are said to be isotopes of that particular element. The sum of the protons plus neutrons is called the atomic mass. The second most common isotope of Lithium on Earth is illustrated below, with an atomic mass of 6, compared to the atomic mass of 7 in the illustrations of lithium above (the atomic mass 7 version is also reproduced below along with atomic mass 6 lithium). Make sure you can figure out which is which!

Figure: Two isotopes of lithium

 

Got it? Then try to challenges below.

 

Bonds:

Below is a bare-bones review of the most basic types of bonds, ionic and covalent.

Understanding bonding depends on understanding that electrons around the nucleus of an atom have energies that are quantized, meaning that they will take on specific energy values and not other values. So, we can think of different energy levels of electrons around the nucleus (which we might call 'energy shells'). An atom's energy state is most favorable (lowest) when particular numbers of electrons are in the shells. Stable forms occur when the atom is surrounded by 2 electrons in the inner shell, or 8 in the next shell out, or 8 in the next shell out after that, as illustrated conceptually in the drawing below where the inner circle is the nucleus, electrons are shown by dots, and the outer dots and circles indicate the energy shells.

Figure: Stable electron configurations for atoms

 

In ionic bonds, the atoms achieve the 'energetically favorable' configuration by trading electrons--or one atom giving up electrons to achieve the favorable configuration and another atom taking those electrons to achieve its favorable configuration. Thus, the number of electrons in the outer shell will drecrease for one atom and increase for the other. This results in the atoms becoming charged (becoming ions) and the opposite charges attract, creating a bond. This kind of bond is most common for atoms that only have to give up or take on 1 or two electrons in order to get to their favorable configuration. The example below shows a sodium atom giving up one 'bare' electron to a flourine atom that takes that electron to complete its energetically favorable configuration.

 

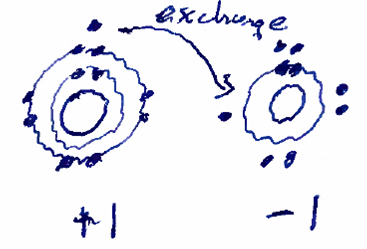
Figure: Ionic bond illustration, sodium and flourine, each ion ends up with 8 electrons in their outer shell due to the exchange

In covalent bonds, the atoms achieve the 'energetically favorable' configuration by sharing electrons, (that is, two or more-electron-pairs are shared between two atoms), increasing the number of electons in the outer energy shell of both atoms. Although this does not create negatively and positively charged ions that attract in the same way as for the ionic bond, the more stable energy level of both atoms when in this configuration makes for a very strong bond. This kind of bond is more common in atoms whose number of electrons puts them right in the middle between two different stable configurations such that gaining or losing a couple of electrons doesn't allow it to reach its favored configuration.

The example below shows a silicon atom, with 4 electrons in its outer shell, sharing electron pairs with two oxygen atoms, which each have 6 electrons in their outer shell.

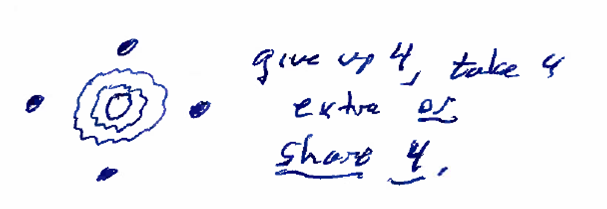
Figure: Inital silicon configuration with 4 outer-shell electrons

 

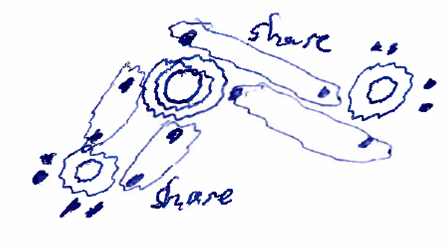
Figure: Covalent bond illustration: Silicon (shown in the center) sharing electrons with two oxygens (shown on either side)--each atom has a total of 8 electrons in the outer shell due to the sharing.

 

The illustration above of bonding between 1 silcon and 2 oxygens, where each oxygen share 2 paris of electrons with the silicon, is not actually what we see in minerals in nature. In the mineral quartz, the silicon atom shares 1 pair of electrons with 4 different oxygen atoms, and then, to reach its favorable configuration, each oxygen atom must share its other 'bare' electron with a different silicon atom. You can see this in the picture of a quartz model below, with black balls for silicon and red for oxygen. Notice that silicon is bonded to 4 oxygen (each bond being a shared pair of electrons), and each oxygen is bonded to 2 silicons (each bond being a shared pair of electrons). The bond angles and distances work together to create a regular, repeated arrangement of atoms called a lattice. All minerals have a crystal lattice--a regular arrangement of atoms.

Figure: Ball-and-stick model of quartz, with silicon represented by black balls and oxygen by red balls, with bonds represented by silver metal sticks connecting them. The black sticks are outlining a unit cell--the smallest unit of the lattice that has all of the characteristics of the lattice. NOTE: The ball-and-stick model does not accurately represent the relative sizes of different atoms!

 

There are other types of bonds in addition to covalent and ionic bonds, such as hydrogen bonds, VanderWaals bonds, and metallic bonds, that result from distributions of electrons among adjacent atoms that differ from either the "exchanged" or "shared" models of the ionic and covalent bonds. In general, these bonds are not as strong as the covalent and ionic bonds, with a rough order of 'strength' often being: Covalent, Metallic and Ionic, Hydrogen, and VanderWaals, although there is a great deal of variability and some ionic bonds are stronger than some covalent bonds. VanderWaals bonds typically are present in very soft materials, such as graphite and some clay minerals.

Coordination Numbers:

Suppose we ask the question: "How many atoms can I pack around another, central, atom (such as in a crystal lattice)?"

We can easily imagine that the bigger the central atom, and the smaller the surrounding atoms, the more atoms that we can pack around the central one, as seen in the pictures below.

This effect results in the idea of a coordination number: the number of 'closest neighbors' that are packed around a particular atom in a crystal.

If we consider oxides and silicates--two important rock-forming groups of minerals--the primary anions that surround cations are oxygen ions. Thus, we can think about the coordination number of the cations (positively charged ions in the crystal) as being the number of surrounding oxygens.

 

More details of 3-dimensional coordination numbers

When the cation is quite a bit smaller than the anion, only a few anions can fit around the cation, and we have a coordination number of 4:

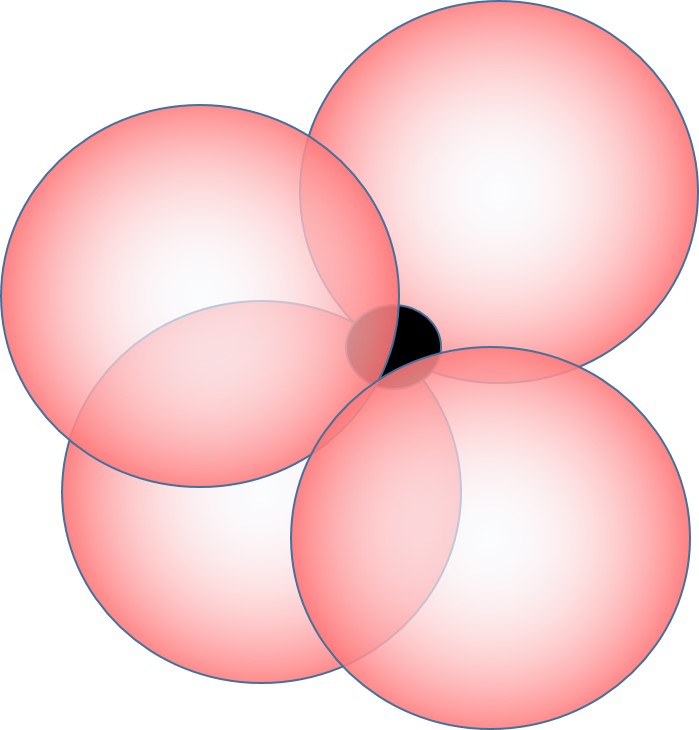
This is also called tetrhedral coordination because the 4 nearest neighbors define the 4 apexes of a tetrahedron with the cation in the center of the tetrahedron.

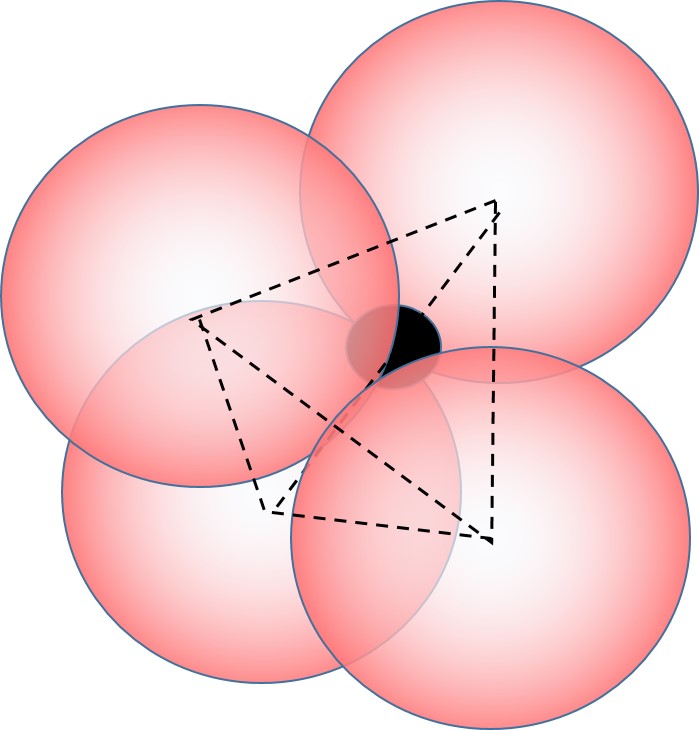
Tetrahedral coordination occurs when the ratio of sizes of cation/anion is generally less than 0.414 (and greater than 0.225).

 

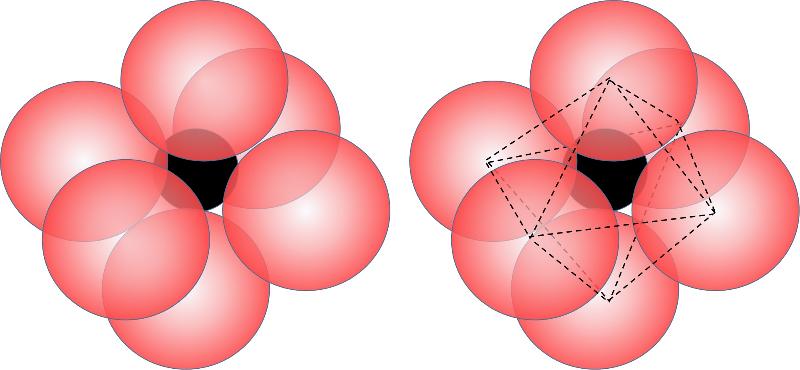
When the cation is a bit bigger in relation to the anion (generally a ratio of cation/anion size from 0.414 to 0.732), then more anions will fit around the cation and we get a coordination number of 6, also called octahedral coordination because the 6 anions define the apexes of an octahedron, as shown below. (Notice that an octahedron has 6 corners but 8 sides).

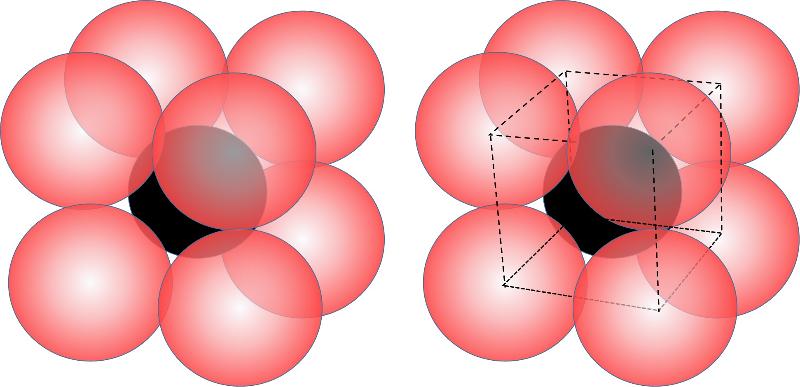
When the cation is bigger still in relation to the anion (generally a ratio of cation/anion size from 0.732 to 1.0), then more anions will fit around the cation and we get a coordination number of 8, also called cubic coordination because the 8 anions define the apexes of a cube, as shown below.

 

If the ratio of cation size to anion size is 1 or greater (that is, if the cation and anion are of similar size), the coordination number may be 12 or larger. A coordination number of 12 cooresponds to the closest packing of spheres, that is, the mostly tightly packed that spheres of equal size can be.

To visualize this, consider 6 anions around a cation in a plane (planar closest packed when they are the same size)

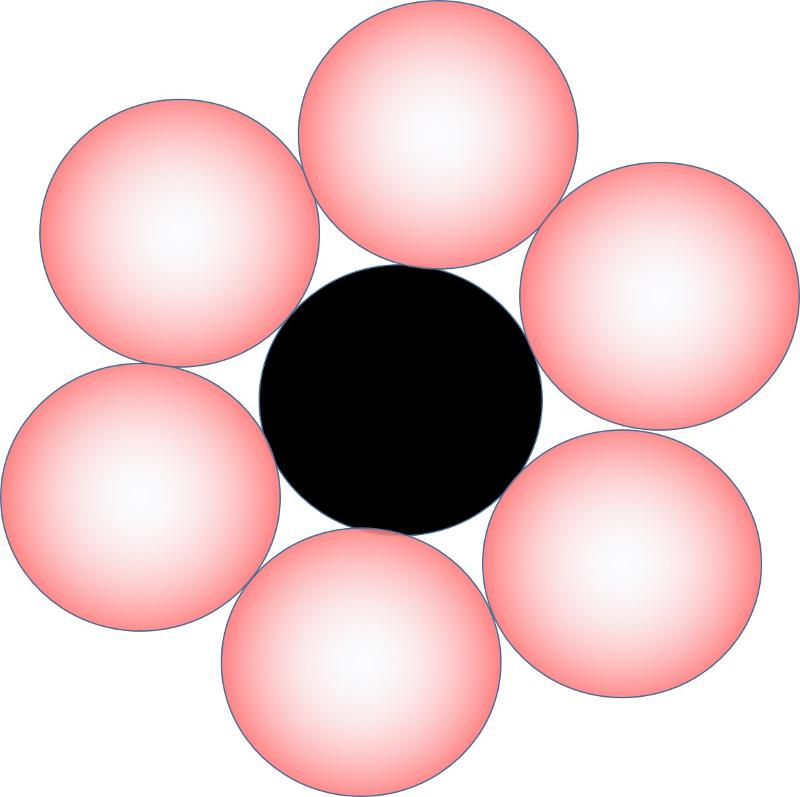
Now think about tucking 3 more anions underneath this plane, the anions fitting into the gaps made by the anions and cations, as shown below.

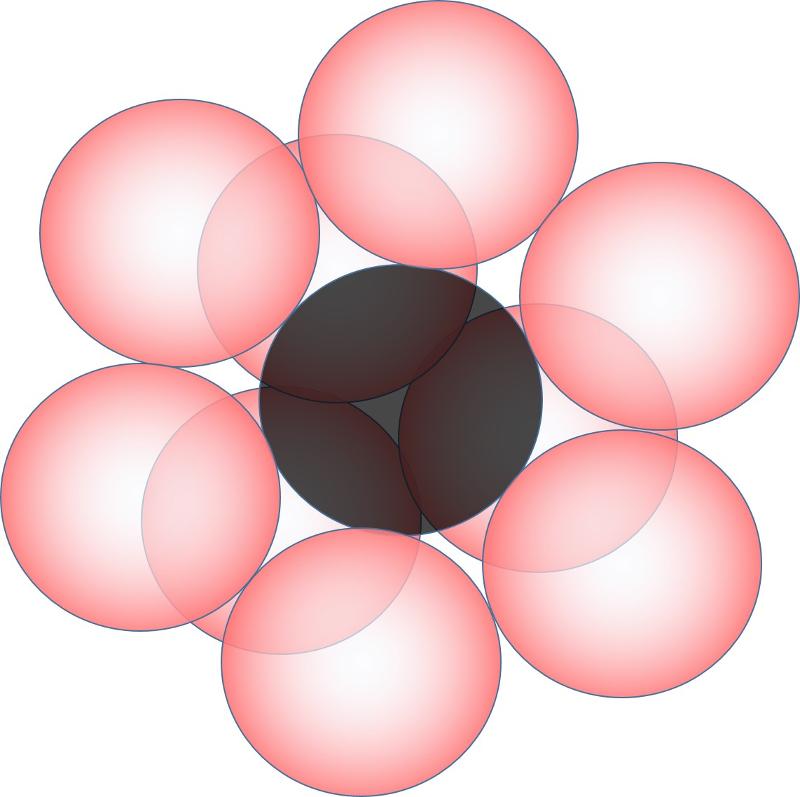
Finally, think about tucking 3 more anions above the original plane of cations and anions. Notice that there are two different ways to do this. 1) you could tuck them in directly above the anions that are underneath the plane. or 2) you could tuck them into the alternate set of gaps in the cations and anions. These are the two different types of closest packing, called hexagonal (1) and cubic (2) closest packing. The picture below shows the second option, which also shows one way to get 12-coordinated cations.

 

 

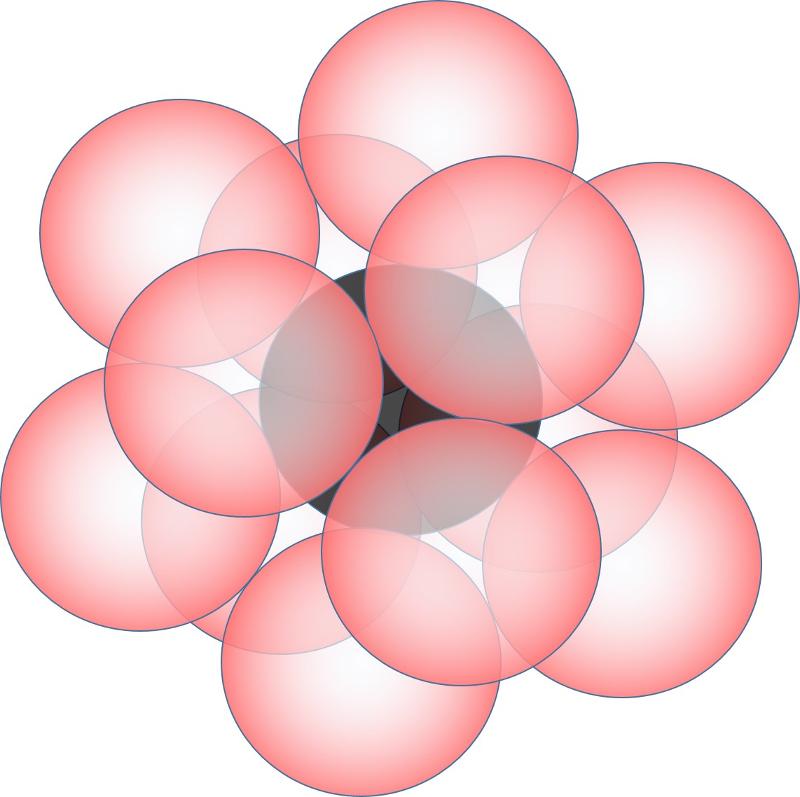
 last updated 8/23/2022.   Text and pictures are the property of Russ Colson.