Mineralogy-3-Dimensional Symmetry and Crystal Systems
Earth Science Extras
by Russ Colson
Portion of a quilt made by my wife, Mary Colson. The basic pattern of squares has a high degree of symmetry (p4mm), although the overall symmetry is lowered by the pattern of colors and the quilting pattern itself, which includes ammonite-shell spirals in the center of each square, leaving us with a symmetry of p1 and no obvious unit cell smaller than the size of the quilt.
Introduction
In the previous lesson on symmetry, we looked at the symmetries and 'crystal groups' in two-dimensions. In this lesson, we are going to look at symmetries and crystal systems in three-dimensions.
In our previous mineralogy lectures, while thinking about the crystal structure of minerals, we have thought about atoms and how those atoms are connected together.
For example, we thought about atoms when we talked about coordination number--the number of nearest-neighbor atoms in a crystal. Na and Cl in a halite crystal, for example, have a coordination number of 6--each Na atom is surrounded by 6 Cl atoms, a coordination that we also call octahedral coordination because the shape it defines has 8 sides. We considered the tetrahdral (4 nearest neighbors) coordination for Si in the very-important silicon tetrahedra and how Si tetrahedra may share more or fewer corners with other tetrahedra, making up the major groups of silicates, the nesosilicates, inosilicates, phyllosilicates, tectosilicates, and so on.
We also thought about atoms when we considered that for many oxide and hydroxide minerals we can think of the crystals as being a closest-packed array of oxygen atoms (or hydroxyl groups), with cations fitting into the spaces between the closest packed oxygens. These interstitial spaces might have tetrahedral (4 nearest neighbors) or octahedral (6 nearest neighbors) coordination with surrounding oxygens. We examined the idea of the charge balance for trioctahdral (periclase and brucite) and dioctahedral (corundum and gibbsite) configurations in this light
We also thought about atom configurations when we considered how to judge whether or not a particular formula was possible for minerals such as pyroxene, feldspar, or garnet. For pyroxene, for example, we considered the chemical formula to be of the format M2M1T2O6, where M1 and M2 are octahedral sites in the crystal and T are tetrahedral sites. M2 is 'stretchier" than M1 and so can sometimes accept bigger cations. Constraints on what formulae are possible includes overall charge balance for the formula, whether the formula has the correct sites filled (M2, M1, and T, for every 6 oxygens), and some consideration of size and charge of cations (remember Goldschmidts Rules that atoms must be of similar size and charge to substitute into a crystal structure--although we can have charge-balancing substitutions).
However, humans began their study of minerals long before they kniew of atoms. Mineralogy is one of the oldest sciences, perhaps second only to astronomy. Examination of minerals began with a consideration of the symmetries revealed in how crystals grow or how they break apart. The symmetry and pattern of minerals, seen in the patterns of crystals faces and cleavage planes, and later in the patterns that emerge from X-ray diffraction, reveal the internal symmetries of the atoms and the basic shapes that make up crystals.
Our lessons below examine the diffferent symmetries and shapes possible in three-dimensional crystals, focusing mainly on the crystal systems (shapes that fill up space) with some consideration of the space groups (shapes plus different motifs with tranlation, glide, and new 3-D processes of srew and inversion).
As in our previous lesson, the basic outline for this lesson, and some of the language used, is provided in the chart below
Crystal Symmetries in Three Dimensions
Going into the kind of detail with 3-dimensional crystals that we did with 2-dimensional crystals isn't possible in this lesson. Not only is symmetry harder to visualize in 3-D, but the number of possible symmetry configurations increases exponentially. For example, we looked at each of the 17 2-dimensional plane groups in theprevious lesson on 2-dimensional crystals, but their are 230 equivalent space groups in 3-D--far more than we could examine individually. Our focus in this lesson will be to practice visuallizing 3-D types of symmetry, recognizing the shapes that make up crystals in 3-D based on their characteristic symmetry, and thinking about a few symmetry operations that occur in 3-D but not in 2-D.
Shapes that fill up space
Analogous to the 4 shapes that fill up space in 2-D (square, rectangle, rhombus, oblique), there are 6 shapes that fill up space in 3-D. These shapes are called Crystal Systems. There are 6, plus, I am adding in the rhombohedral system, a subset of hexagonal.
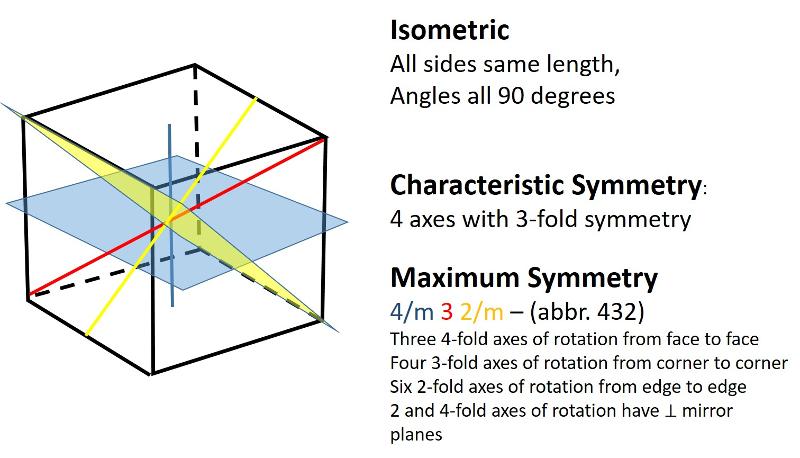
Isometric (unit cell like a cube): all sides are of equal length and angles between sides are 90 degrees
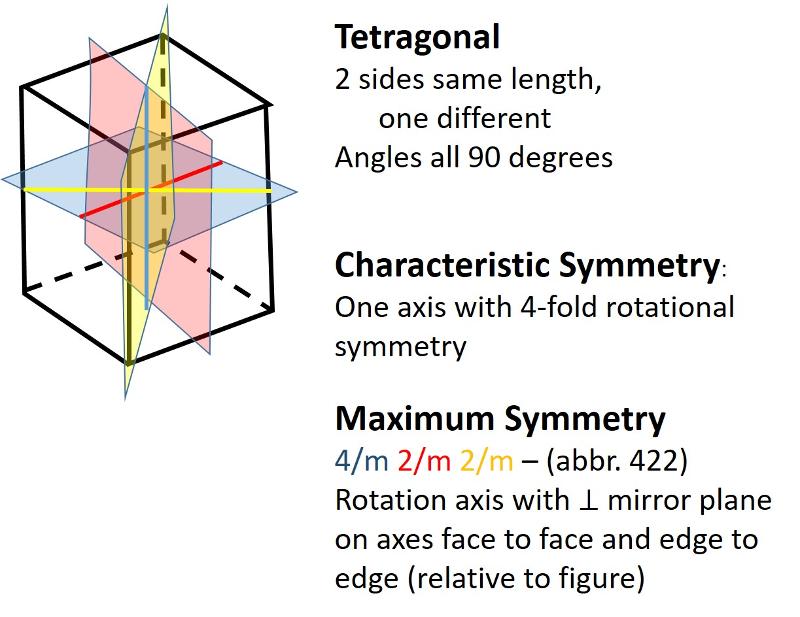
Tetragonal (unit cell like an elongated or shortened cube): One side has a different length from the other two sides which are equal. Angles between sides are again 90 degrees.
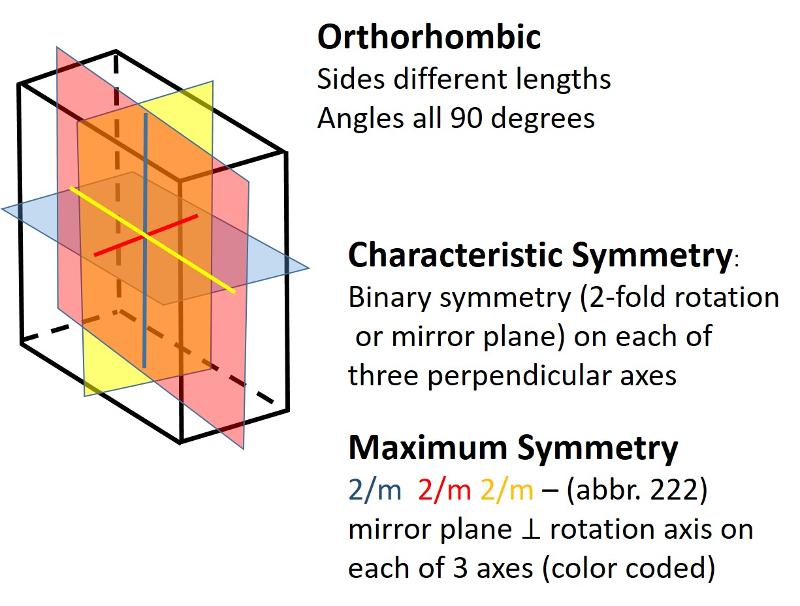
Orthorhombic (unit cell like a cube elongated or shortened in 2 dimensions): All sides are different lengths. Angles between sides are again 90 degrees.
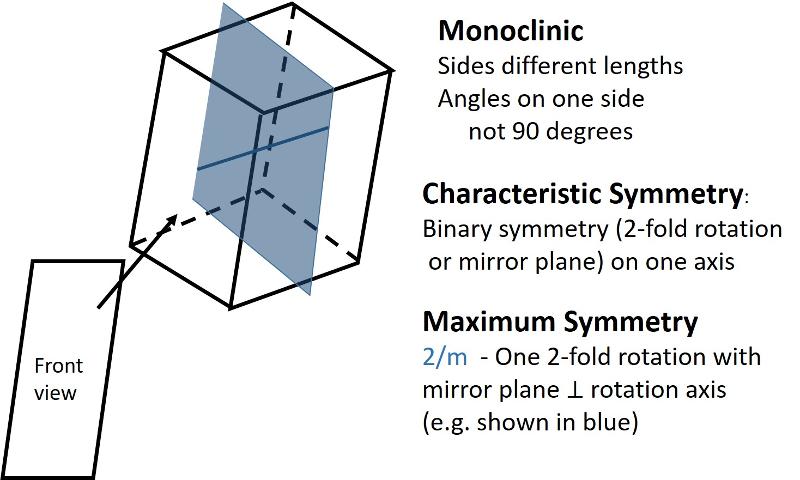
Monoclinic (unit cell like a cube sheared-over in one direction): All sides can be different lengths. Of the 3 non-parallel sides, the angle between one pair is not 90 degrees, the other two pairs are at 90 degrees.
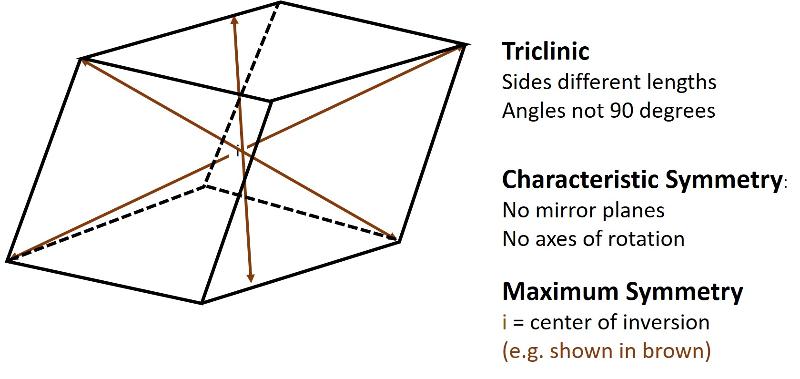
Triclinic (unit cell like a cube sheared over in three-directions). All sides can be different lengths. The angles between the 3 non-parallel sides differ from 90 degrees.
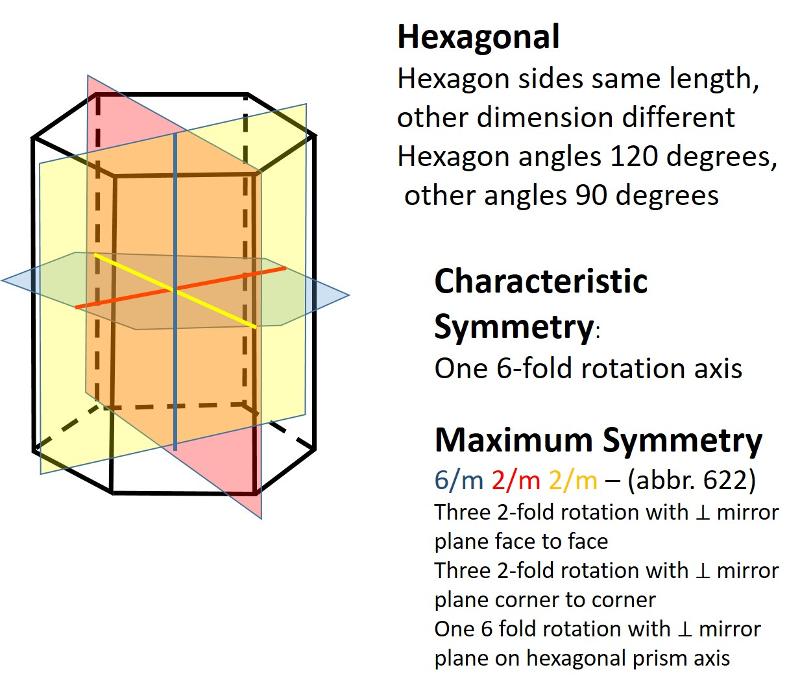
Hexagonal (unit cell like a one-third portion of a hexagonal prism), Length of one axis differs from others, with angles of 120 degrees and 90 degrees)
Rhombohedral (a subset of Hexagonal, but with 3-fold rotation instead of 6-fold, all sides are equal length and all angles differ from 90 degrees)
Below are illustrations of each of these basic shapes for unit cells in three dimesional space.
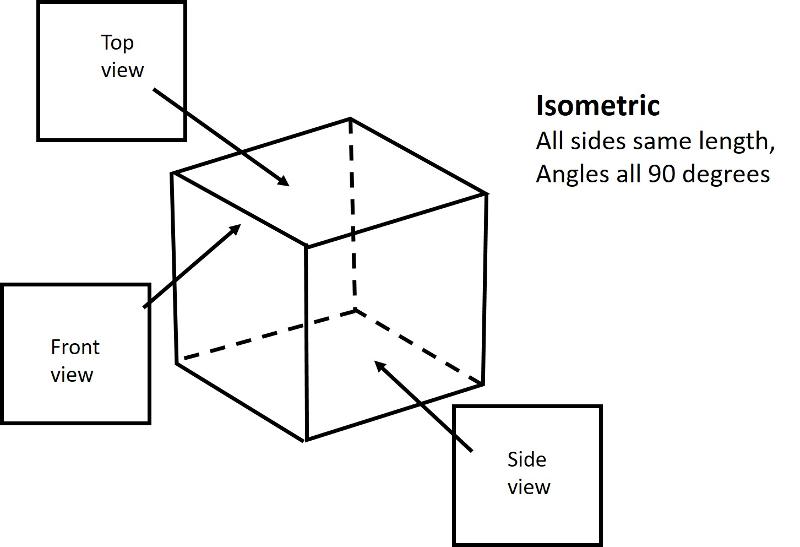
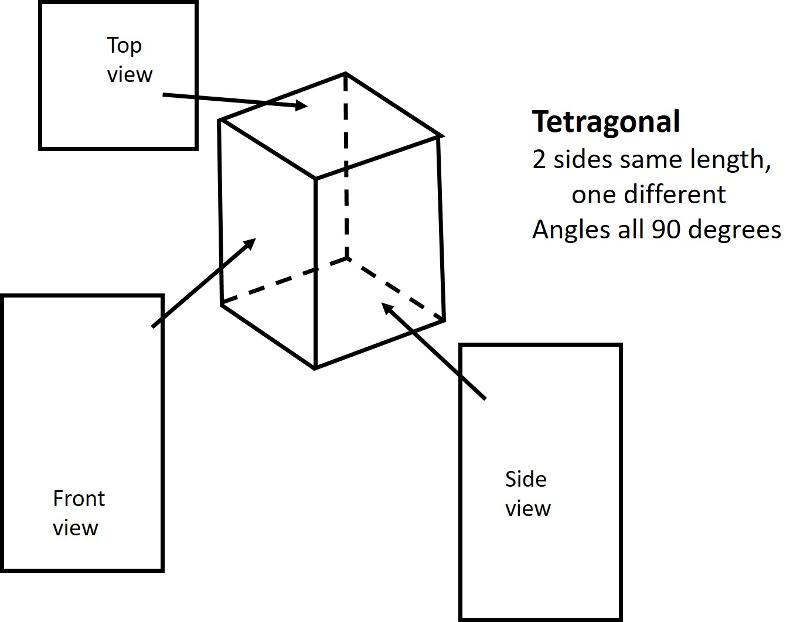
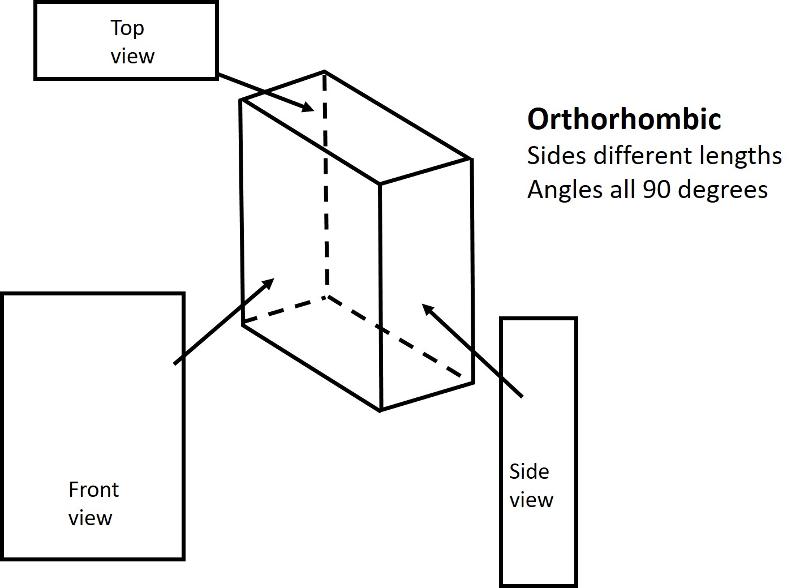
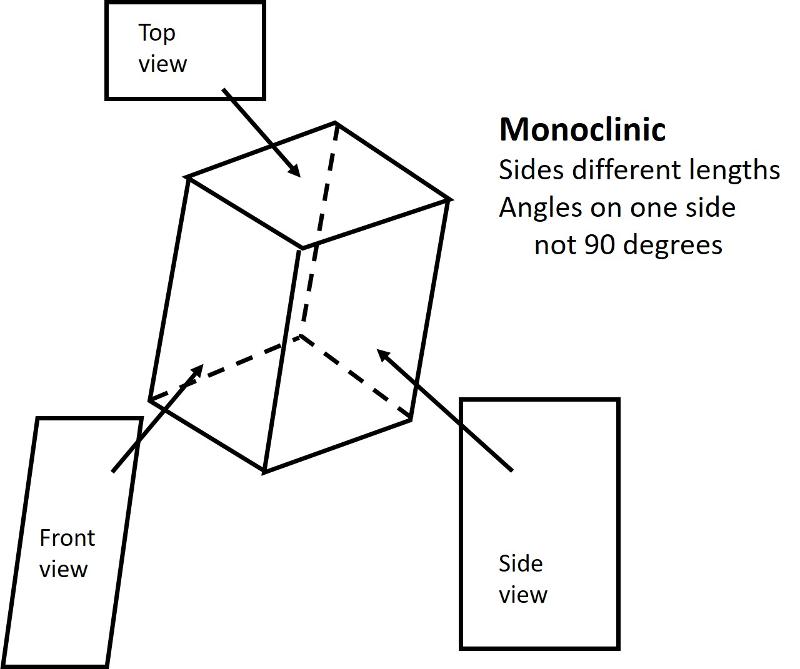
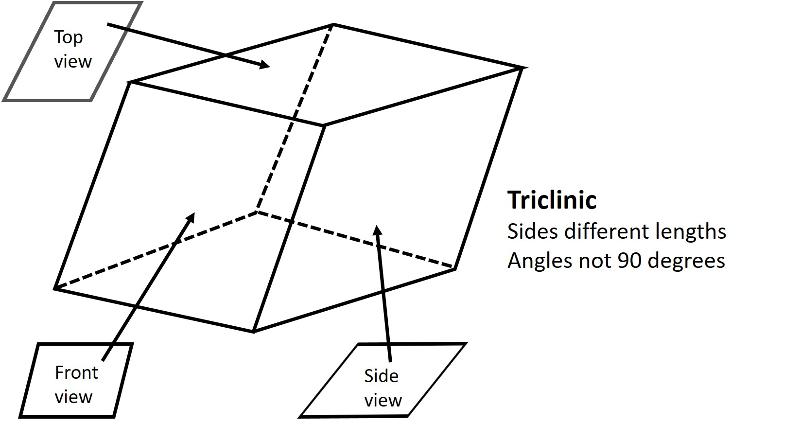
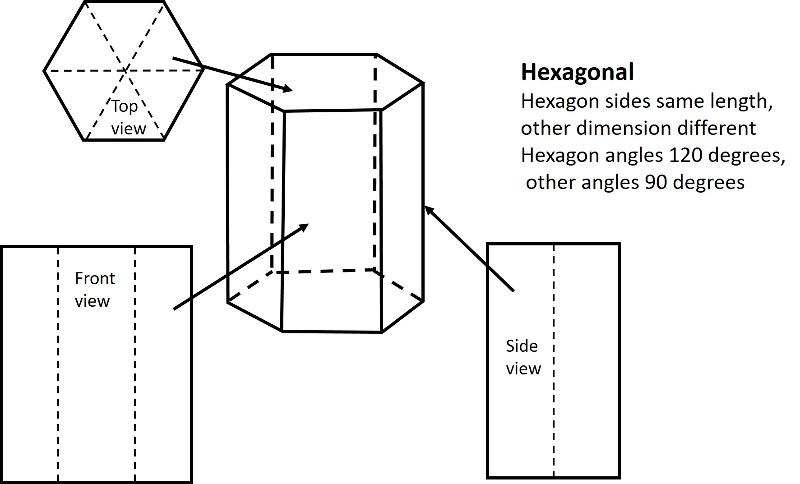
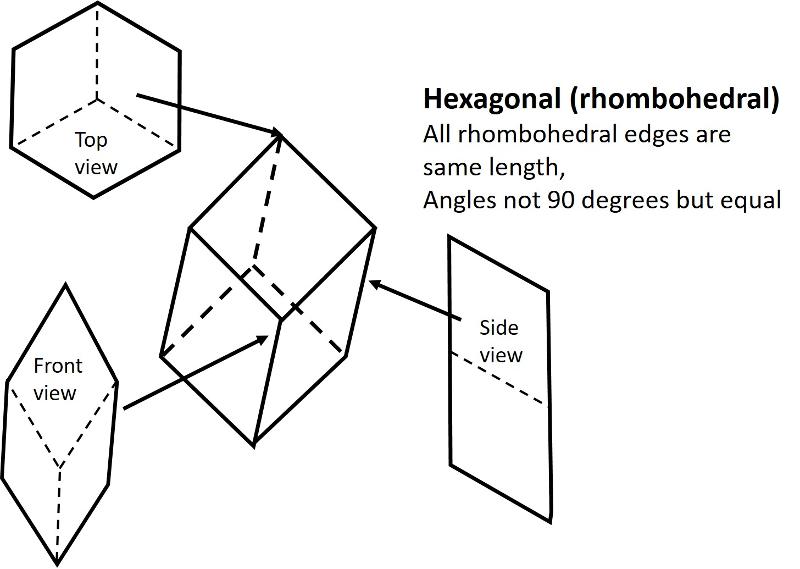
Bravais Lattices
As with patterns in 2-dimensions, lattice points are the points in or on the unit cell to which motifs (patterns, or clusters of atoms) can be copied to reproduce the image. As in 2-dimensions, many of the lattices are simply the basic shapes with lattice points at their corners (although there are more corners in three dimensions!). There are also lattices with points in the center and points in the center of faces. There are 14 Bravias lattices in 3 dimensions--14 possible sets of lattice points that can fill up space with each lattice point having the same pattern around it (that is, the same motif at each lattice point).
The Illustrations of the Bravais Lattices below comes from https://en.wikipedia.org/wiki/Crystal_system
Crystal Classes--Motifs in Three Dimensions
We still find the elements of symmetry in 3-D that we had in 2-D-- 1, 2, 3, 4, and 6-fold axes of rotation and mirror planes. However, those axes can now exist in multiple directions in three dimensional space.
For example, consider a cube. You can easily imagine a 4-fold axis of rotation emerging toward you from the square side of a cube. However, there will now be THREE of those 4-fold axes, one emerging from each pair of faces of the cube (6 faces =three 4-fold axes of rotation). In addition there are 3-fold and 2-fold axes of rotation and quite a number of mirror planes. We often designate the mirror planes relative to a particular axis, so, for example, there might be a mirror plane perpendicular to each of the 4-fold axes of rotation--we would designate this with Hermann-Mauguin notation as 4/m = a 4-fold axis with a perpendicular mirror plane.
The illusration below shows an image of one side of a cube with the corners cut off. The red symbol shows a 4-fold rotation axis emerging from the image toward us. It has a mirror plane perpendicular to it (which we can't see). The other two 4-fold rotation axes are shown in blue and yellow, with their associated mirror planes shown in corresponding color.
Cubes also have 3-fold axes of rotation. You might be thinking, "wait a minute, a cube can't have a three-fold rotation axis can it? Indeed, it can--in fact, four 3-fold rotation axes is the characteristic symmetry for the isometric system. The image below is looking down on one corner of the cube with the cut-off corners, showing the 3-fold rotation axis. Since there are 8 corners in a cube, and the 3-fold axes go corner to corner, we will have four 3-fold axes as shown in the figure below.
Cubes also have 2-fold axes of rotation that go from the center of one edge to the corresponding edge on the other side of the cube. The two-fold axes of rotation can also have mirror planes perpendicular to them. In the image below, only the two-fold axes that we are looking down, plus one other, is shown. The mirror plane for the 2-fold axis shown with a red diamond will not be seen in this perspective. The mirror plane for a different 2-fold axis of rotation is shown in yellow. Since there are 12 edges on a cube, we can see that there are six 2-fold axes in a cube. The blue mirror plane in the figure is perpendicular to a 4-fold axis that is not shown.
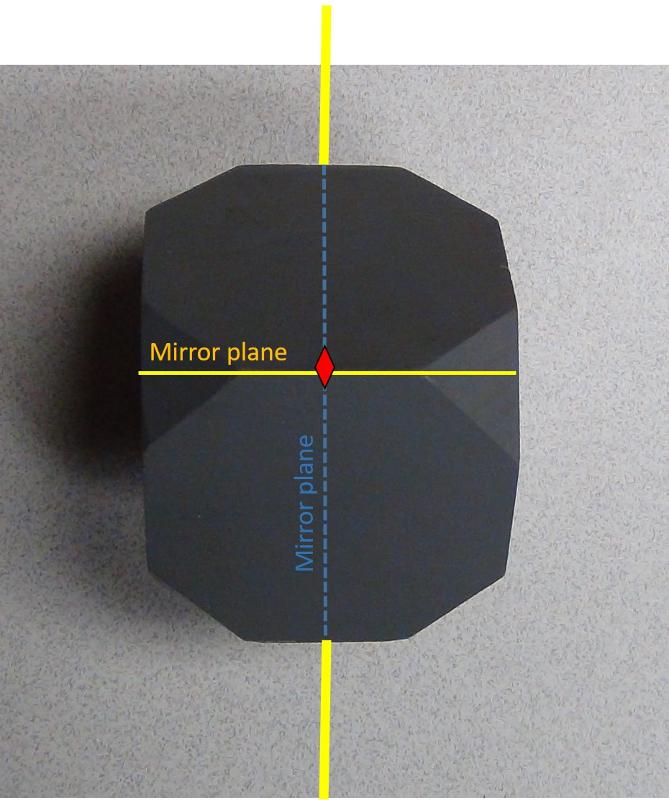
In addition to 3-D figures having more (and more complex) mirror planes and rotational axes, they also have other symmetry operations not important in 2-D. For example, in 3-D we need to consider the center of inversion as a symmetry operation (in 2-dimensions, the center of inversion is not different from rotation). The center of inversion is kind of like reflection, except instead of reflecting across a plane, points are "inverted" through a point in the center of a unit cell. A center of inversion will be illustrated for the triclinic system in the pictures below.
Another symmetry operation that occurs in three dimensions is the operation of rotoinversion--a combination of a partial rotation followed by inversion through the center point. In 2-D, rotoinversion is not different from simple rotation. In 3-D, rotoinversion is often not the same thing as rotation and inversion operating separately. Rotoinversion is best understood and illustrated with the use of stereographic projection, which we are not addressing in this lesson, and therefore we are not going to examine it further, although axes of rotoinversion will be indicated for some of the ball-and-stick models in the exercises below.
In the 2-dimensional exercises in the previous lesson, we identified which basic shapes correspond to particular motifs or unit cells based on characteristic symmetries. We are going to do a similar thing for shapes in three dimensions. First, here are the characteristic symmetries for each of the Crystal Systems (plus rhombohedral), along with some illustrations of the symmetries of the most symmetrical members of each crystal system. There is quite a bit of information in these illustrations, but be sure to get the idea of the characteristic symmetry--the symmetry element that all members of that particular crystal system share. Notice also that some of the other symmetry elements are color coded to help you make the connection between the Hermann-Muaguin notation and symmetry elements in the unit cell. As promised, the center of inversion is illustrated for the triclinic system.
Identify the crystal system for each of the shapes below based on their characteristic symmetries.
Shape 1:
Click on the video to get symmetry data
Shape 2:
Click on the video to get symmetry data
Shape 3:
Click on the video to get symmetry data
Shape 4:
Click on the video to get symmetry data
Shape 5:
Click on the video to get symmetry data
Shape 6:
Click on the video to get symmetry data
Shape 7:
Click on the video to get symmetry data
Shape 8:
Click on the video to get symmetry data
Shape 9:
Click on the video to get symmetry data
Shape 10: Ignore minor flaws in symmetry.
Click on the video to get symmetry data
Shape 11:
Click on the video to get symmetry data
Shape 12:
Click on the video to get symmetry data
Shape 13: Ignore writing
Click on the video to get symmetry data
Shape 14: Ignore differences in coloration and writing--only consider shape.
Click on the video to get symmetry data
Shape 15:
Click on the video to get symmetry data
Shape 16:
Click on the video to get symmetry data
Shape 17:
Click on the video to get symmetry data
Shape 18: ignore variations in color, materials, and writing--only consider shape
Click on the video to get symmetry data
Shape 19:
Click on the video to get symmetry data
Shape 20: ignore minor imperfections in this hand-made shape
Click on the video to get symmetry data
Shape 21: Ignore minor imperfections in this hand-made shape
Click on the video to get symmetry data
Shape 22:
Click on the video to get symmetry data
Shape 23:
Click on the video to get symmetry data
We have only considered a handful of the 32 Crystal Classes--mainly the most highly-symmetrical crystal class from each crystal system--these are the patterns that most resemble the basic shapes that fill up space (although we have looked at a couple of shapes with lower symmetry).
Needless to say, even for these simplified highly-symmetrical patterns, the motifs and patterns can get a lot harder to recognize when we are looking at atoms connected to each other by bonds, rather than simple shapes. However, the concept of looking for symmetry is similar. The invention of X-ray diffraction allowed us to infer the crystal structure of many minerals by their atomic positions rather than simply by the external pattern of crystal faces and cleavage planes.
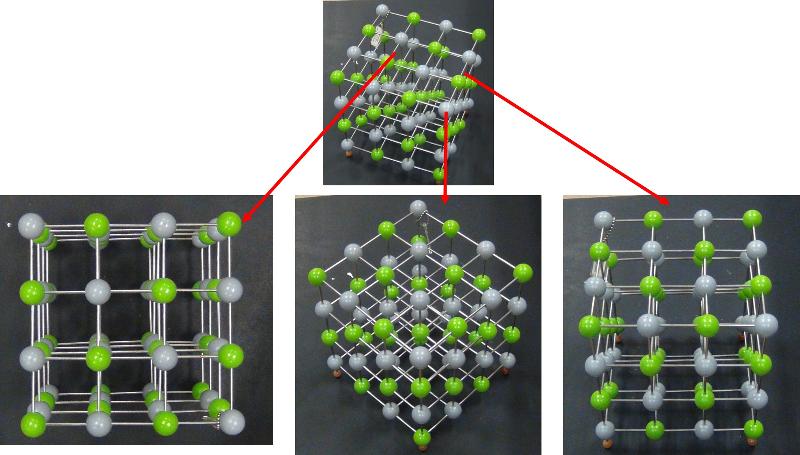
Here is a simple ball and stick model with unit cells not marked out and symmetry not specifically shown. Can you identify the crystal system?
Space Groups
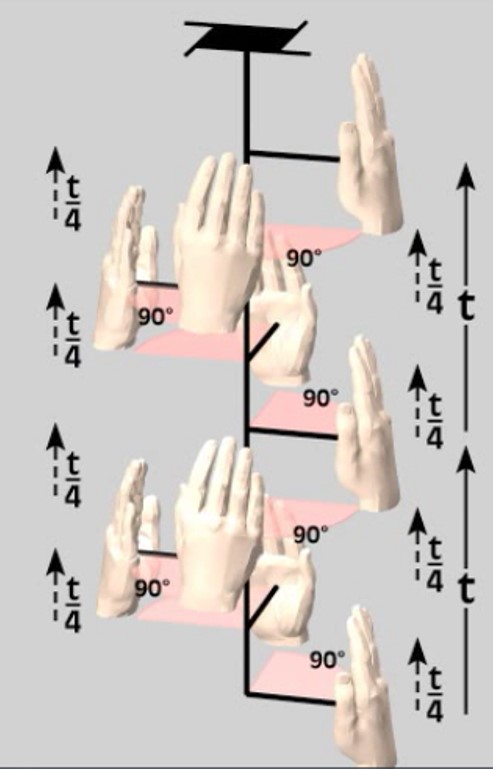
Two hundred and thirty possible space groups are way more than we can look at individually in this lesson. Like the Plane Groups were a set of all possible patterns derived by combining the lattices with the point groups (motifs), taking into account translation and glide operations, so the Space Groups are the set of all possible symmetries derived by combining the Bravais Lattices with the Crystal Classes (motifs), taking into account translation, glide, and a new process called screw that operates in three dimensions but not in 2-D. Like glide was a combination of translation and reflection, screw is a combination of translation and rotation. An illustration of a 4-fold screw axis is provided below from https://serc.carleton.edu/NAGTWorkshops/mineralogy/xtlsymmetry/elements.html, showing rotation around the axis in steps of 90 degrees combined with translation vertically along the axis.
Here is a list of the 230 space groups from our textbook Mineral Science, 23rd edition, by Klein and Dutrow. Look at the Herman-Mauguin designation and see how much you can figure out. A number with a bar over it refers to an axis of rotoinversion. A number with a subscripted number (e.g. 64) refers to a screw axis (with the numbers giving information about the type of screw axis). Substituting a letter (e.g. a, b, c, d, n) for an 'm' refers to a glide plane, with the letters giving information about the axis (or axes) on which the glide occurs (a, b, and c for glide along one of these axes, or n and d for glide in multiple directions). Notice that the space groups have the same form as the corresponding crystal class, but include glide planes and screw axes. The initial letters give information about which Bravais lattice is involved (P=primitive cell with lattice points only on the corners, F= lattice points in centers of faces [or A, B, or C for lattice points only in the center of selected faces], I= lattice point in center of figure, R= rhombohedral lattice points.
To focus more on the connecting the Hermann-Mauguin notation to particular Crystal Systems (the basic shapes), try to connect the following Crystal Classes with the correct Crystal System.
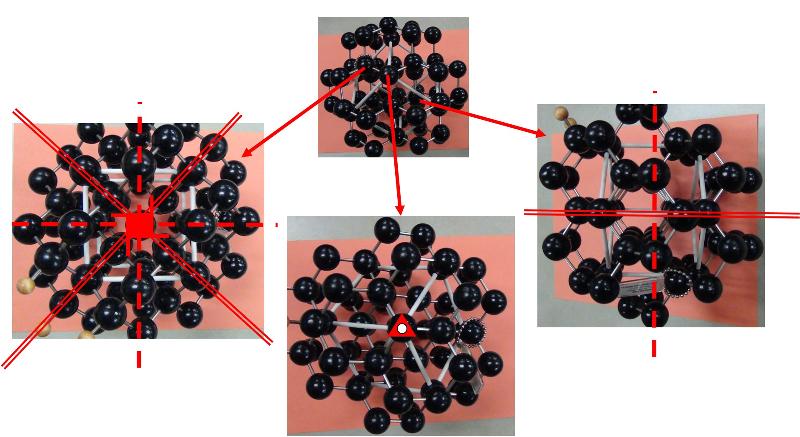
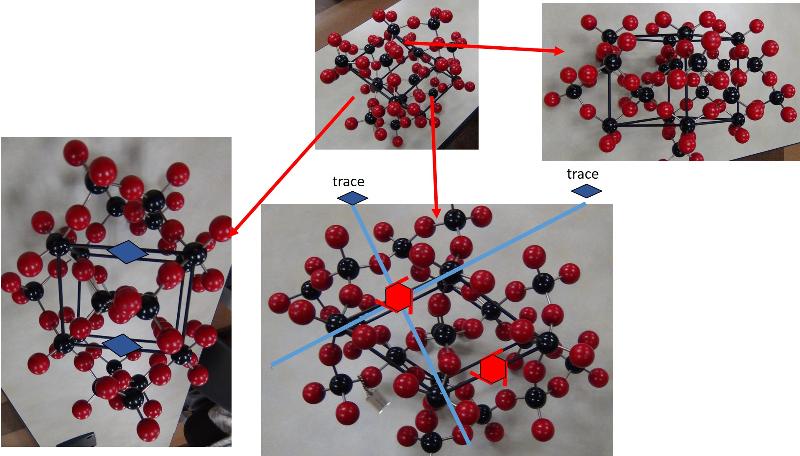
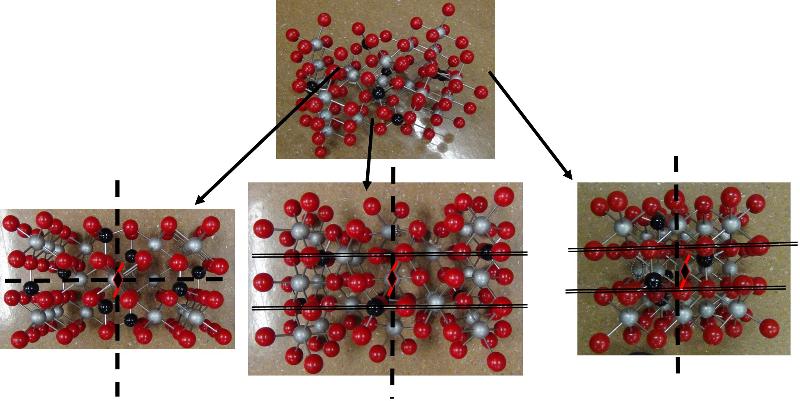
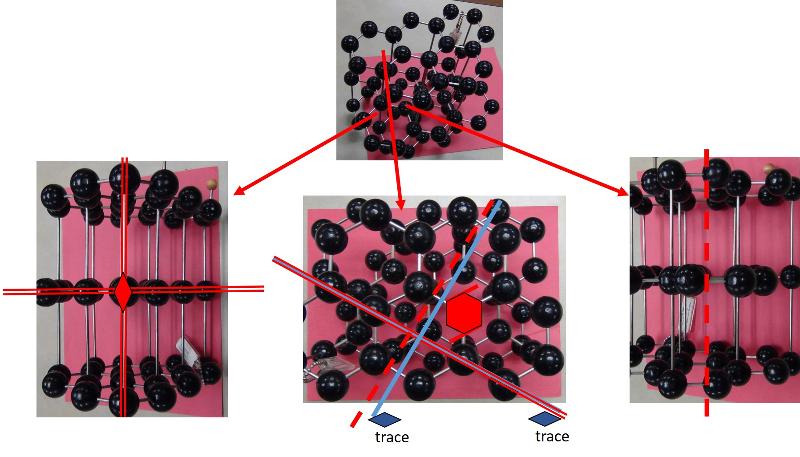
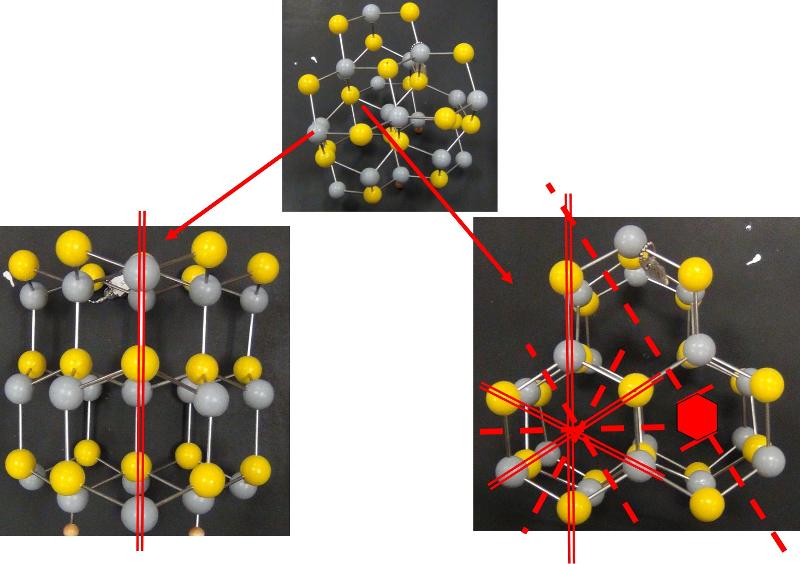
Looking at arrays of atoms in three dimensions to infer the space group is much harder than simply recognizing basic crystal systems based on solid shapes. This is something that probably only specialists in crystallography or other material science fields get truly good at, but some practice at it can help with spatial thinking skills and give a sense of how we think about crystal structures at the atomic level. In the ball-and-stick models below, I have added in my best estimates for some of the key symmetries for each crystal pattern, using the standard symbols: two parallel lines to indicate a mirror plane, a solid dashed line to represent a glide plane, appropriate symbols for axes of rotation (axes of rotoinversion have a dot in the middle, screw axes have 'legs' on the sides of the rotation symbol). In some cases, I have shown the trace of an axis of rotation rather than looking down the axis itself. Remember that the mirror plane associated with a particular axis is perpendicular to the axis, and thus will show up in a different perspective from that looking down the axis. Look at these patterns--can you see them? Could you find them in a ball-and-stick model? In doing this exercise myself, I did not start with the model and figure out the symmetries, but rather started with the known symmetries and tried to find them in the models--it was still pretty hard to do. so, practice, practice, practice!
Identify the Space Group for each of the following crystals from the list below, based on the symmetries shown.
last updated 12/20/2020. Text and pictures are the property of Russ Colson except where specifically noted in the text. Other imagery comes from Crystal System at https://en.wikipedia.org/wiki/Crystal_system, https://serc.carleton.edu/NAGTWorkshops/mineralogy/xtlsymmetry/elements.html, and Mineral Science, 23rd edition by Klein and Dutrow.
