Mineralogy- 2-Dimensional Symmetry, Lattice Systems, and Plane Groups

Earth Science Extras

by Russ Colson

 

Portion of a quilt made by my wife, Mary Colson. The basic pattern of squares has a high degree of symmetry (p4mm), although the overall symmetry is lowered by the pattern of colors and the quilting pattern itself, which includes ammonite-shell spirals in the center of each square, leaving us with a symmetry of p1 and no obvious unit cell smaller than the size of the quilt.

Introduction

Humans began their study of minerals long before they kniew of atoms. Mineralogy is one of the oldest sciences, perhaps second only to astronomy. To start with, people were fascinated by the symmetries seen in the way that crystals grow. Symmetry has had a profound impact on human thought, showing up in artwork for thousands of years. The symmetry and pattern of minerals, seen in in andcient times in the patterns of crystals faces and cleavage planes and later in the patterns that emerge from X-ray diffraction, reveal the internal symmetries of the atoms and the basic shapes that make up crystals.

Our lessons below examine how we have come to think about symmetries and the shapes that makeup the possible building blocks of crystals. To help understand the concepts, we are going to first focus on 2-dimensional 'crystals', and then, in a later lesson, apply those ideas to understanding crystals in 3-dimensions.

The basic outline for these two lessons, and some of the language used, is provided in the chart below 

 

 

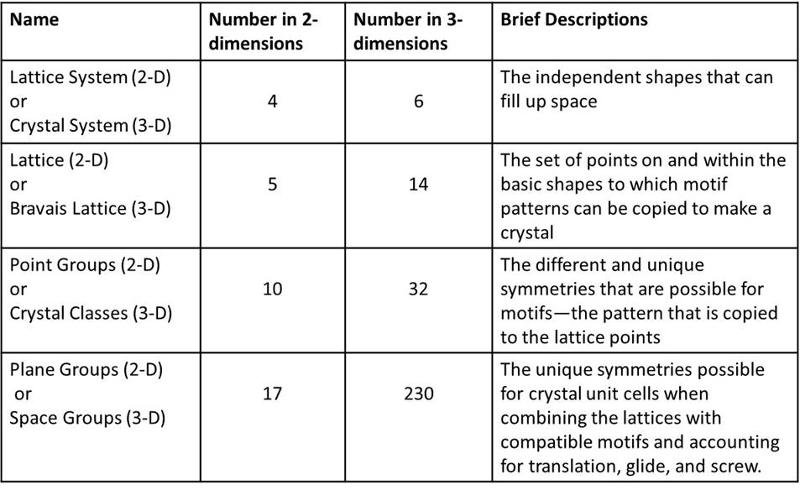
Crystal Symmetries in Two Dimensions

Shapes that fill up space

Only some shapes can fill up space in two dimensions. For example, when you go to the hardware store to buy tile, you don't buy tile of any shape, but only the shapes which, when fit together, will completely cover your floor.

 

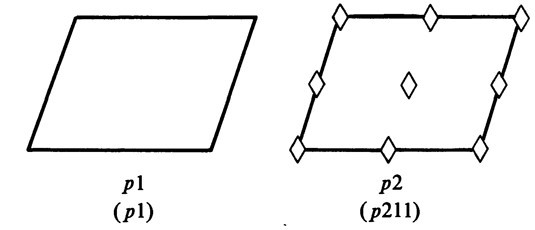
Although lots of shapes can fill up space, there are only 4 shapes that are independent--that is, all other shapes that fill up space can be made by a combination of these 4. These four are the following:

1) square

2) rectangle

3) rhombus

4) parallelogram (which we call oblique)

These are the four basic shapes called lattice systems listed in the introduction above.

You might be thinking, "but wait, what about the hexagon--doesn't it fill up space?" Well, yes, but the angles between the sides of the hexagon equal 120°, and the angles of the rhombus also equal 120°, and so the hexagon can be manufactured from the rhombus--thus the hexagon is not an independent shape.

 

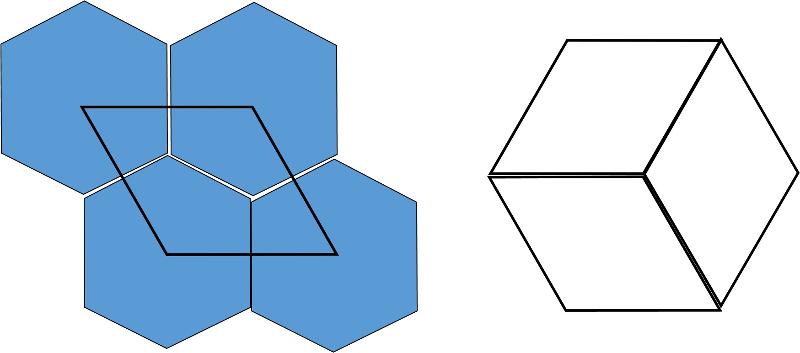
Likewise, any triangle, when reversed and copied so that it can fill up space, becomes either a square, rectangle, rhombus, or parallelogram.

You might also be thinking, "but wait, isn't the square just a special case of the rectangle (in which all sides have equal length), and the rhombus just a special case of the parallelogram (in which all sides have equal length and angles that are 120° and 60°?" Well, yes, in a way. But the symmetries of the square and the rhombus are quite different from the rectangle and parallelogram, and so it makes sense to identify them as different shapes.

 

What do we mean by symmetries?

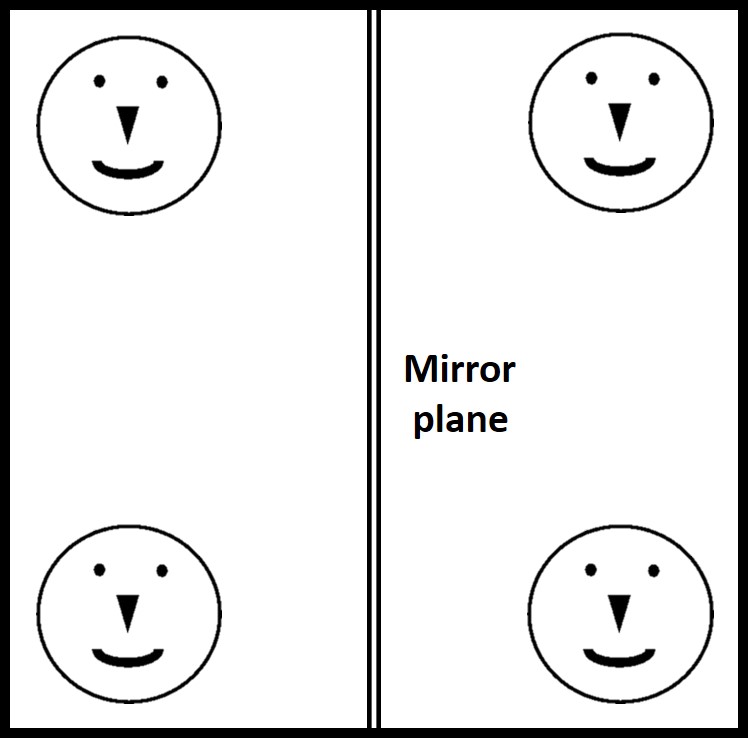
Two key symmetry operations are the mirror plane and the axis of rotation.

A mirror plane is an imaginary plane that can be drawn through a shape such that one side of the shape looks exactly like a reflection of the other side.

 

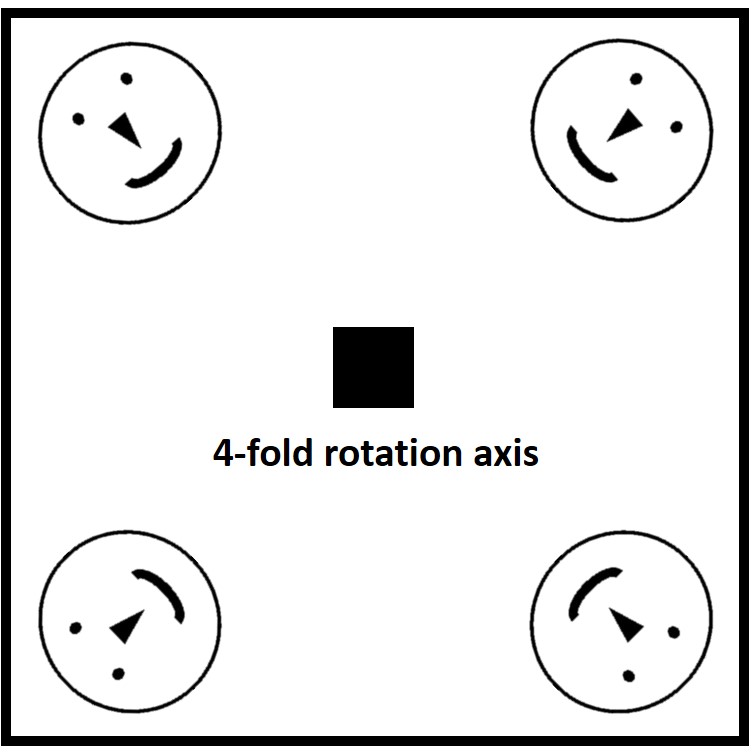
An axis of rotational symmetry is a an imaginary axis drawn through shape such that rotation around this axis yields basically the same view several times in a single rotation.   For example, looking down on a square with the axis of rotation coming up at us from the center, it can be seen that we get basically the same view 4 times as we rotate it, thus this is a 4-fold axis of rotational symmetry.

 

Unit Cell

A unit cell of a crystal in either 2 or 3 dimensions can be thought of as the smallest shape that fills up space and that contains all of the symmetry and properties of the crystal as a whole. This unit cell can be copied and moved (translated) to recreate the entire crystal structure without overlapping or leaving gaps. In a 3-D crystal, the unit cell is a collection of atoms (from a few atoms to maybe 1000 for some of the largest unit cells), that have a fixed geometry relative to each other and encompass the overall symmetry of the crystal. For 2-D 'crystals', the unit cell encompasses all of the unique elements of a pattern such that copying that unit cell will reproduce the entire pattern. The unit cell should have the same symmetry as the overall pattern.

 

Consider the wallpaper below (for sale on Amazon in Nov, 2020). Which of the shapes provides the best unit cell, according to the unit cell criteria listed above? (smallest possible size, matching symmetry, no overlaps or gaps)

 

Consider the wallpaper below (for sale on Amazon in Nov, 2020). Which of the shapes provides the best unit cell, according to the unit cell criteria listed above?

 

Consider the wallpaper below (for sale on Amazon in Nov, 2020). Which of the shapes provides the best unit cell, according to the unit cell criteria listed above?

 

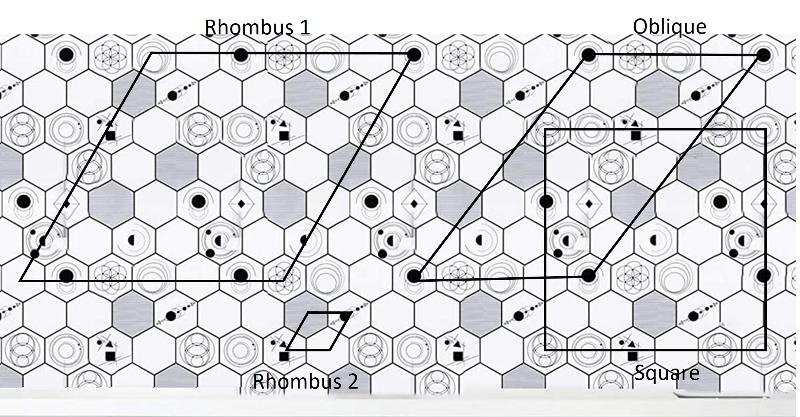
Consider the wallpaper below (for sale on Amazon in Nov, 2020). Which of the shapes provides the best unit cell, according to the unit cell criteria listed above?

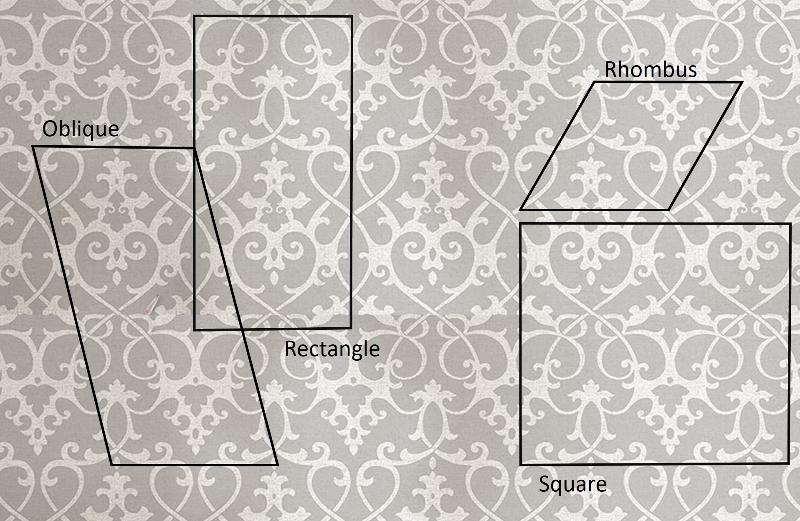
Consider the wallpaper below (for sale on Amazon in Nov, 2020). Which of the shapes provides the best unit cell, according to the unit cell criteria listed above? (smallest possible size, matching symmetry, no overlaps or gaps)

 

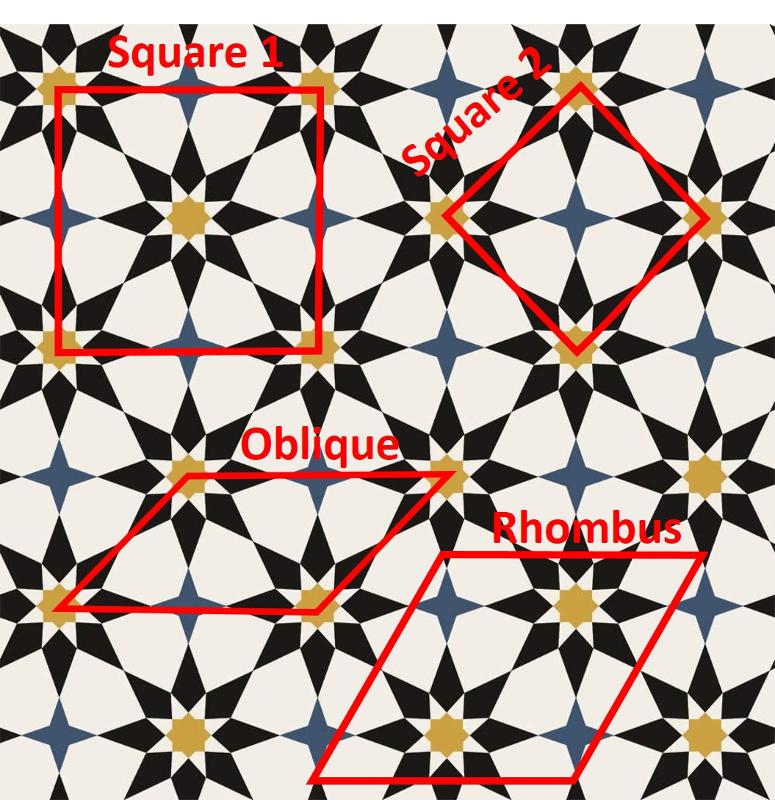
Lattice Points

Lattice points are the points in or on the unit cell to which motifs (patterns, or clusters of atoms) can be copied to reproduce the image. As seen in the table at the beginning of this lesson, there are 5 lattices in 2-dimensional 'crystals'--that is, only one more than there are basic shapes that fill up space. Notice the dots on the shapes below, indicating that these are lattices with lattice points shown, not simply the shapes that fill space.

The five lattices in two dimensions are the following:

Square System :

 

Rhombus System:

 

Oblique System:

 

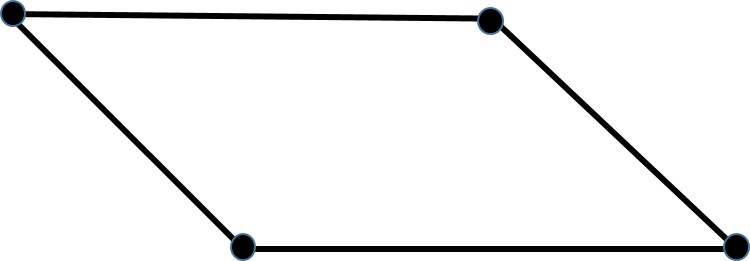
Rectangular System:

 

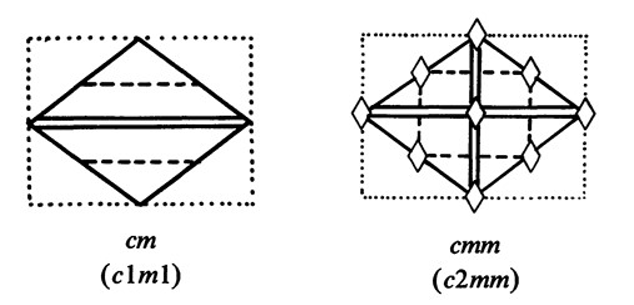
Centered Rectangle System:

 

Notice that the lattice for each of the first four basic shapes is simply the shape with lattice points on the corners. The fifth lattice is the rectangle with an extra lattice point in the center, called a centered rectangle.

 

That gives us all five! You might be wondering why we can't put points in the middle of the other shapes and get a uniquely different lattice. The reason can be understood with a bit of spatial thinking. A point in the middle of the square simply gives us 4 smaller squares, so not uniquely different from the square (For example, in the pattern with the 8-pointed flowers above, we had an option for a centered square, but the better and smaller choice was the smaller square). Symmetry constraints don't allow us to put points in the middle of the other two shapes because putting a motif at that locaton would disrupt the symmetry of the pattern.

Sometimes the centered rectangle is portrayed as a diamond. The resulting diamond also has all the information in it needed for a unit cell (the symmetry and pattern content). Below is an illustration:

 

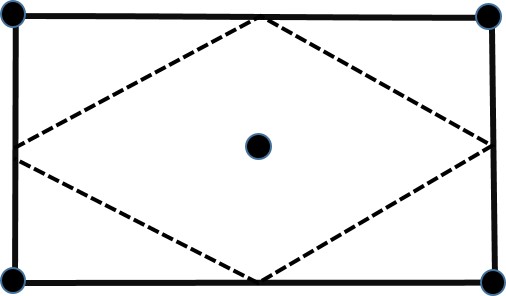
The example centered rectangle below shows the diamond. This illustration is rotated to correspond with the illustration above, but the rectangle has different dimensions. Notice that there is enough information in the diamond to reproduce the entire pattern. Also notice that the motif (the bird) is the same around all five of the centered-rectangle lattice points--one at each corner and one in the center. Thus, this illustration also shows the meaning of motif in terms of a set of lattice points.

In this lesson, I tend to stick with the centered rectangle rather than the diamond because the diamond can be easily confused with a rhombus or oblque, even though it has quite different symmetry and implications for the character of the pattern.

 

Point Groups (the motifs)

There are 10 possible types of motif in 2-dimensions, that is, 10 unique types of symmetry. These 10 are illustrated below in symbolic form.

 

This motif has no mirror planes and its maximum symmetry is an axis of 1-fold rotation (in other words, it has to be rotated back to its original position to look the same). It is designated by the number "1", meaning, 1-fold axis of rotation.

This motif has no mirror planes, but it has a 2-fold axis of rotation. The narrow diamond shape is the standard symbol marking the location of a 2-fold axis of rotation. This motif is designated by the number "2" meaning, 2-fold axis of rotation.

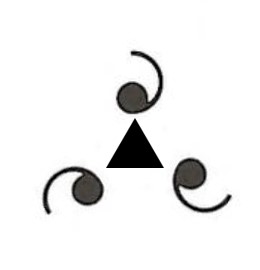This motif has no mirror planes, but it has a 3-fold axis of roatation. The triangle is the standard symbol marking the location of a 3-fold axis of rotation. This motif is designated by the number "3", meaning, 3-fold axis of rotation.

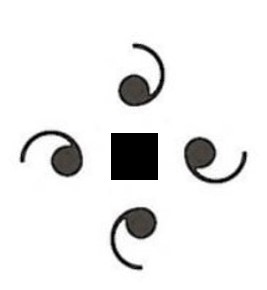This motif has no mirror planes, but it has a 4-fold axis of rotation. The square is the standard symbol marking the location of a 4-fold axis of rotation. This motif is designated by the number "4", meaning, 4-fold axis of rotation.

This motif has no mirror planes, but it has a 6-fold axis of rotation. The hexagon is the standard symbol marking the location of a 6-fold axis of rotation. This motif is designated by the number "6", meaning, 6-fold axis of rotation.

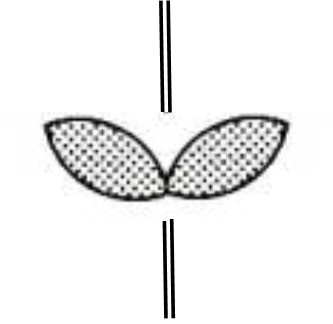This motift has no axis of rotation, but has one mirror plane. The location of the mirror plane is shown by a double line. This motif is designated by the letter "m", meaning, mirror plane.

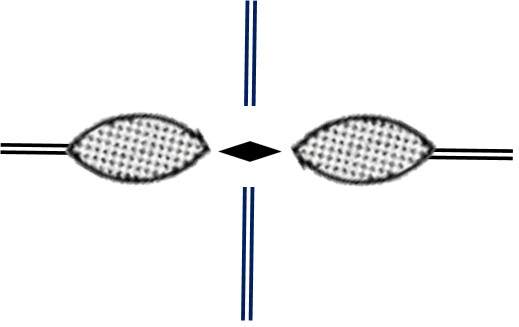This motif has a 2-fold axis of rotation, shown with the standard symbol, and two different types of mirror planes, one marked with black double lines that pass through the markers, and one marked with blue double lines that pass perpendicular to the first mirror plane. This motif is designated by "2mm", meaning, 2-fold axis plus two types of mirror planes.

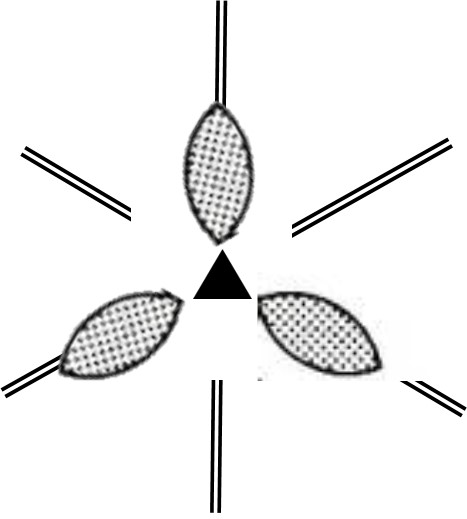This motif has a 3-fold axis of rotation, shown with the standard symbol, and a single type of mirror plane (copied three times by the rotational symmetry). The mirror planes are marked with black double lines. This motif is designated by "3m", meaning, 3-fold axis plus one type of mirror plane.

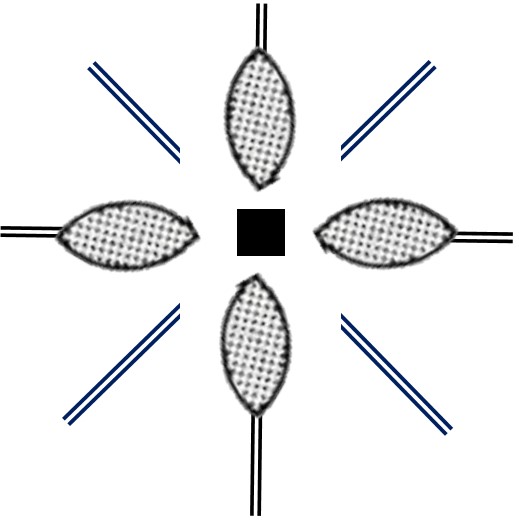This motif has a 4-fold axis of rotation, shown with the standard symbol, and two different types of mirror planes, one marked with black double lines that pass through the markers, and one marked with blue double lines that pass diagonally between the first mirror planes. The symmetry of rotation means that there are four mirror planes, two of each type. This motif is designated by "4mm", meaning, 4-fold axis plus two types of mirror plane.

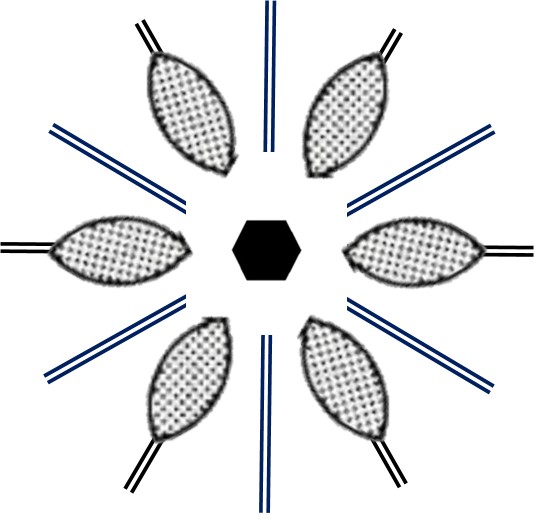This motif has a 6-fold axis of rotation, shown with the standard symbol, and two different types of mirror planes, one marked with black double lines that pass through the markers, and one marked with blue double lines that pass diagonally between the first mirror planes. The symmetry of rotation means that there are 6 mirror planes, three of each type. This motif is designated by "6mm", meaning, 6-fold axis plus two types of mirror plane.

 

 Plane Groups

There are 17 possible types of patterns in two dimensions when we combine the 5 possible lattice systems with the 10 possible motifs and consider the effects of glide (to be defined below). You might be thinking, "wait, if there are 5 possible lattice systems and 10 possible motifs, then there should be 5 x 10 = 50 possible plane groups (plus whatever extra we get with the whole 'glide' thing".

 

That doesn't happen because some motifs are incompatible with some lattice systems. To understand this, let's first consider the characteristic symmetry of each lattice system.

The Oblique System has the lowest symmetry. It's characteristic symmetry is that it has no mirror planes, no glide planes, and no 3, 4, or 6 fold axes of rotation (it can have 2-fold rotation)

The Rectangle System has as its characteristic symmetry either mirror plane(s) or glide plane(s) (which is like a mirror plane--explained below), but not both.

The Centered Rectangle System has as its characteristic symmetry both mirror plane(s) and glide plane(s)

The Square System has as its characteristic symmetry a 4-fold axis of rotation.

The Rhombus System has as its characteristic symmetry either a 3-fold or 6-fold axis of rotation (or both).

 

It's clear that if we use a motif that does not have 4-fold rotational symmetry, we can't create a plane group in the square system (for example), thus the only motifs that are compatible with the Square System are 4, and 4mm. Other motifs (like 1, 2, 2mm, 3, 3m, 6, 6mm) don't work for the square system. Likewise, the motif "1" can't work for the rectangular system. Motifs 4 and 4mm can't work in the rhombus system. And so on.

 

So, what's a glide plane? A glide plane is a plane of translation combined with reflection (you might think of it as an offset reflection), as shown below.

 

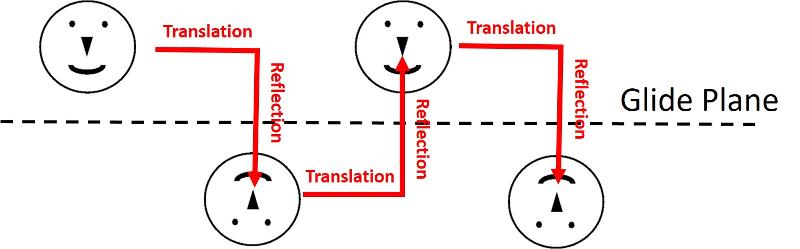
There can be other types of symmetry across the glide plane, such as shown below.

 

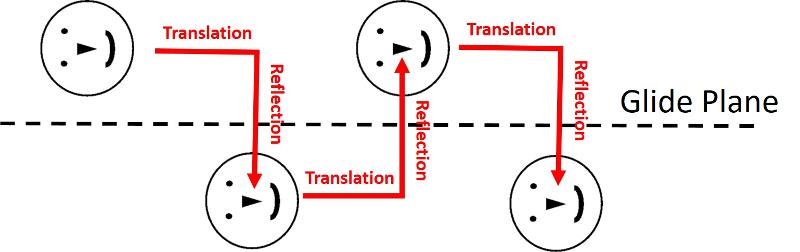
We have already looked at the kind of glide plane symmetry shown above in one of our previous exercises--the bird wallpaper (on sale on Amazon Nov, 2020).

So, what is the lattice system for this pattern? It has no 3, 4, or 6 fold rotation axes, so it's not Square or Rhombus. It has mirror planes and glide planes, so it's not Oblique. It has both mirror planes and glide planes, so it is Centered Rectangle, as previously illustrated above, rather than Rectangle.

 

Before we get into the 17 different plane groups, let's practice identifying the basic lattice system that different patterns belong to based on their characteristic symmetries.

 

We have already been using the Hermann-Mauguin notation for crystal symmetry, that is, using the numbers and letters that indicate axes of rotation, presence of mirror planes, and presence of glide planes. An example of Hermann-Maugin notation is 4mm to designate a 4-fold axis of rotation and 2 different types of mirror planes. Based on the characteristic symmetry for each Lattice System, match up each of the following 2-dimensional Hermann-Mauguin notations with one of the lattice systems.

 

 

Example of how the Plane Groups are derived from the lattice systems, motifs, and glide process:

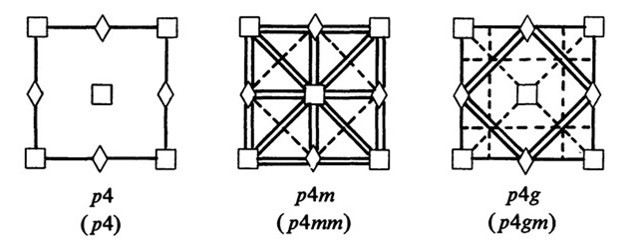
As our example, we are going to look at the plane groups in the square lattice system. There are three and only three plane groups possible in this system. These three are derived by combining the square lattice with the only two motifs that are compatible with the square system (4mm and 4) as shown below.

 

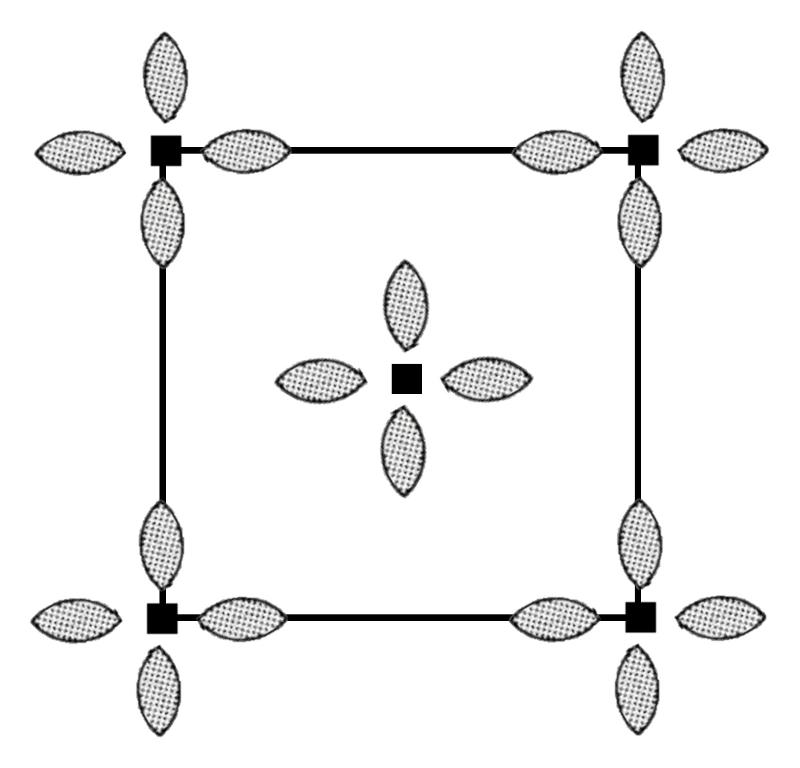
p4mm: This plane group is derived by combining the 4mm point group motif with the square lattice as shown below.

The symmetry of this group reflects the high symmetry of the motif, with two types of mirror planes as shown below (using the double line to indicate a mirror plane). There are also several two-fold axes of rotation which are not shown--can you find them? Also not shown are several implicit glide planes which are not required to produce the image, but are a consequence of the presence of the mirror planes--these pass diagonally between the center and the corners, cutting off each of the corners--for example one passes diagonally from lower left to upper right half way between the center and the upper left lattice point.

 

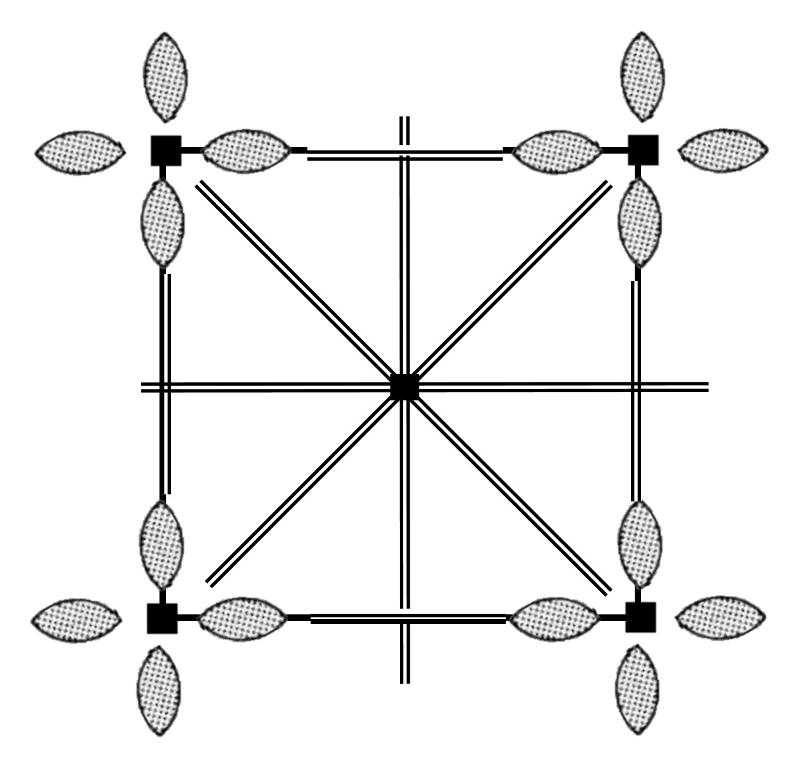
p4: This plane group is derived by combining the "4" point group motif with the square lattice as shown below.

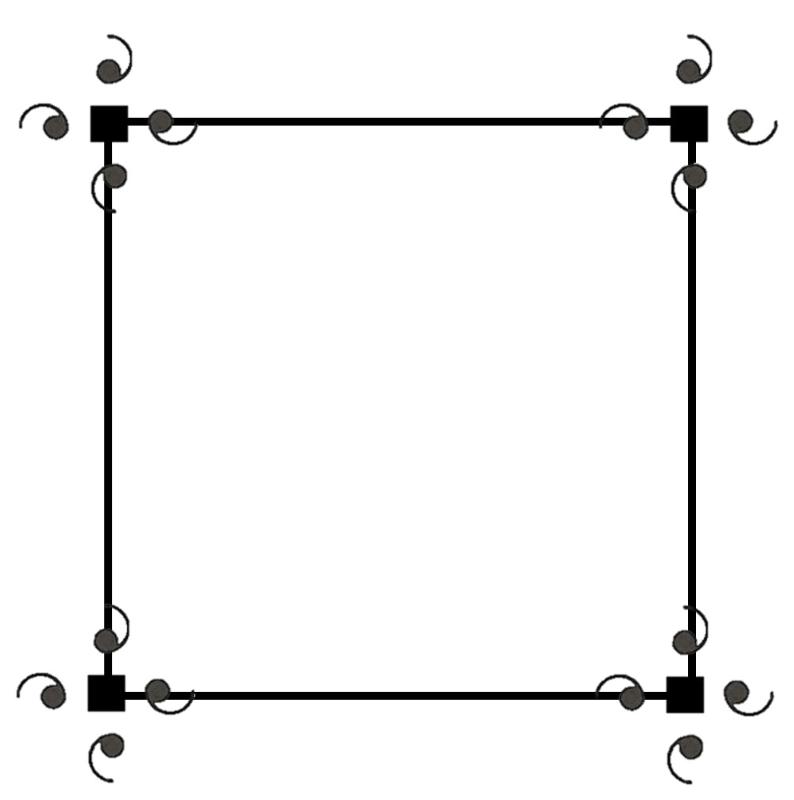
This plane group has 4-fold rotational symmetry, with a 4-fold axis at each corner and in the center. It also has several 2-fold axes (can you find them?), but no mirror planes because the assymetry of the motif prevents mirror symmetry.

 

p4gm: This plane group is derived by combining the "4" point group motif with the square lattice plus a glide plane. The construction of the unit cell from the glide plane is shown in the steps below. Notice how the center pattern is a mirror image of the motif at the four corners.

 

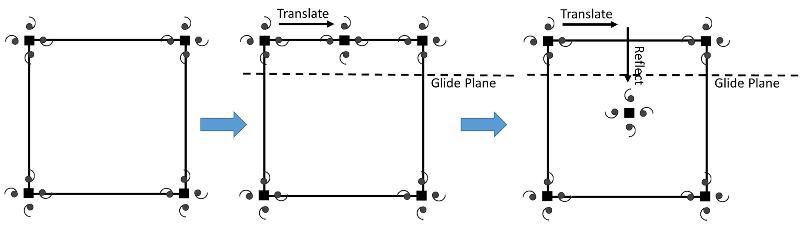
The glide plane results in mirror plane symmetry in this plane group, as shown below (double lines for mirror planes, dashed lines for glide planes). This group also has 2-fold axes of rotation--can you find them?

 

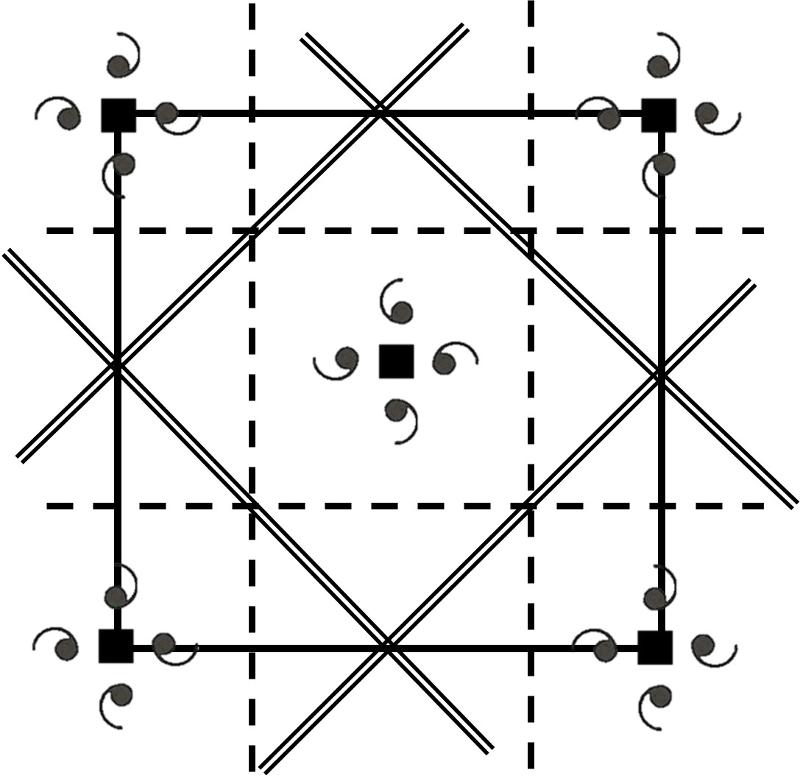
That's it, only these three are possible. You might be asking, "but wait, why don't we have the option of combining the 4mm motif with the square lattice plus a glide plane?

The reason is that the result of that operation is not symmetrically distinct from simply choosing a smaller unit cell that is like p4mm above.

To see this, consider the illustrations below.

 

Unit cell for the 4mm motif copied onto the 4 points of the square lattice, plus a glide plane operation:

Copying this unit cell produces the pattern shown below, in which a smaller unit cell with the same symmetry can be chosen (shown in red) :

 

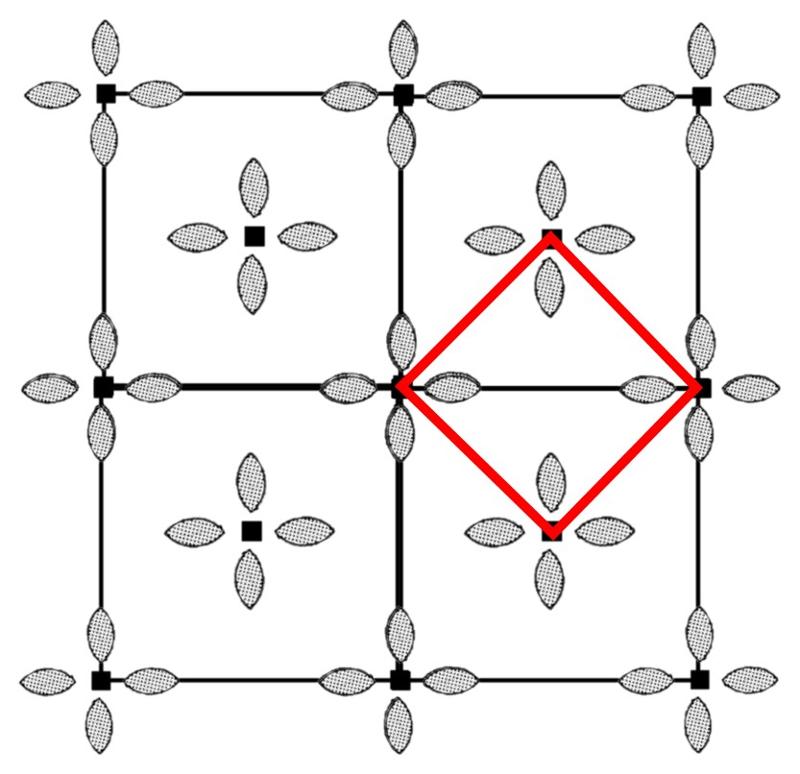
NOTE: This has been a pretty in-depth examination of 2-dimensional "crystals", and we haven't even looked at the 17 Plane Groups yet except for the three plane groups in the square system. If you are worn out, you might skip the next section. But if you want the whole thing (and with all the artwork it should be fun), here it is (there are only three questions in this section, but drawing out the symmetries in each pattern before your try to answer the questions, and then working through my symmetry drawings in the answer feedback, could take 1-3 hours to do properly)!

 

Recognizing the 17 Plane Groups

The big difference between the point groups (motifs) and the plane groups is that the plane groups involve processes of translation and/or glide in copying the motif patterns. We add the letter 'p' before the notation to signal these are refering to a "primitive" lattice (that is lattice points only on the corners of the shapes) or 'c' to signal the lattice is "centered" (that is, a lattice point in the center of the shape). The initial letter also provides a dfference between the notation for the plane groups versus the notation for a point groups (motif): p4mm indicates a plane group, 4mm would indicate the point group with equivalent symmetry.

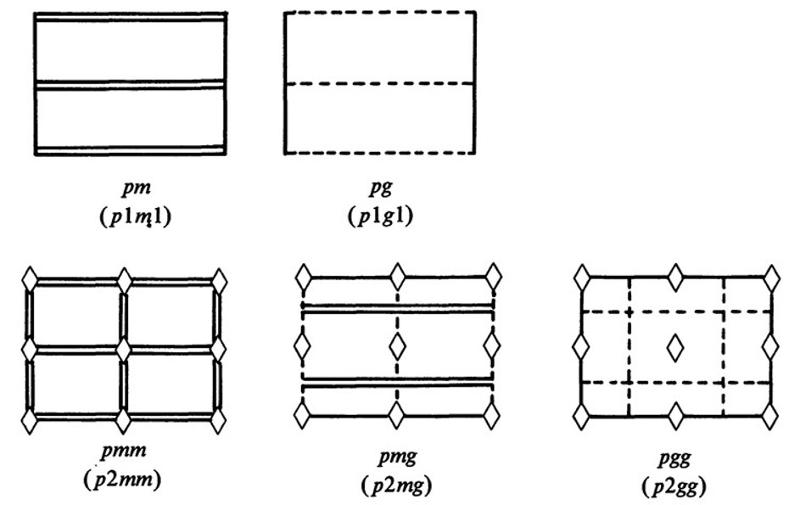
Now that we have some practice recognizing the basic Lattice Systems, let's dig into identifying each of the 17 Plane Groups. The 17 Plane Groups, with their detailed symmetries, are shown below, from "The Plane Symmetry Groups: Their Recognition and Notation", by Doris Schattschneider, 1978, in The American Mathematical Monthly. Symbols for rotational axes are the diamond, triangle, square, and hexagon (for 2- 3-, 4-, and 6-fold) as is standard, double solid lines are used for mirror planes, and dashed lines are used for glide planes. This chart also includes a "short hand" version for many of the notations, with the full version below in parentheses. Each of the 17 different Plane Groups can be uniquely identified on the basis of its symmetry. Study the illustrations below until you have an understanding of the different symmetries of each plane group. Notice that some have no mirror planes, some have no rotational axes, some have no glide planes. Others do have those features, in very specific locations in the unit cell. Some have multiples of those features, again in very specific locations in the unit cell. Notice also that the three plane groups in the square system are the same as the three that we derived in the lesson above.

 

Plane Groups in the Oblique System

 

Plane Groups in the Square System

 

Plane Groups in the Rhombus System (with maximum 6-fold axis of rotation)

 

Plane Groups in the Rhombus System (with maximum 3-fold axis of rotation)

 

Plane Groups in the Centered Rectangle System

 

Plane Groups in the Rectangle System

 

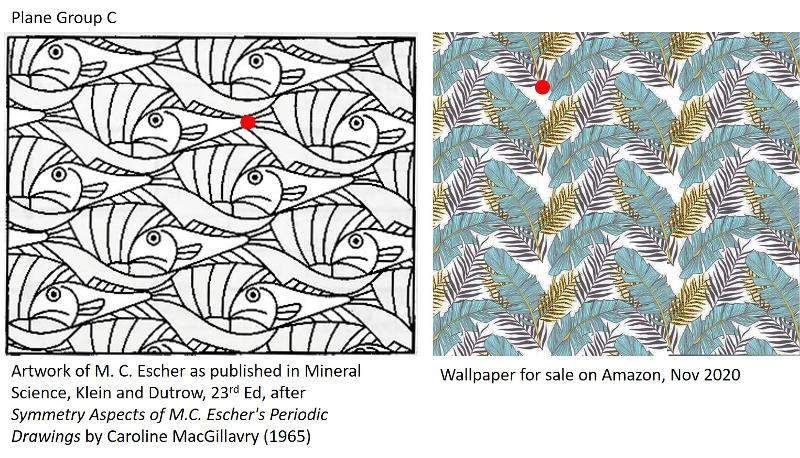
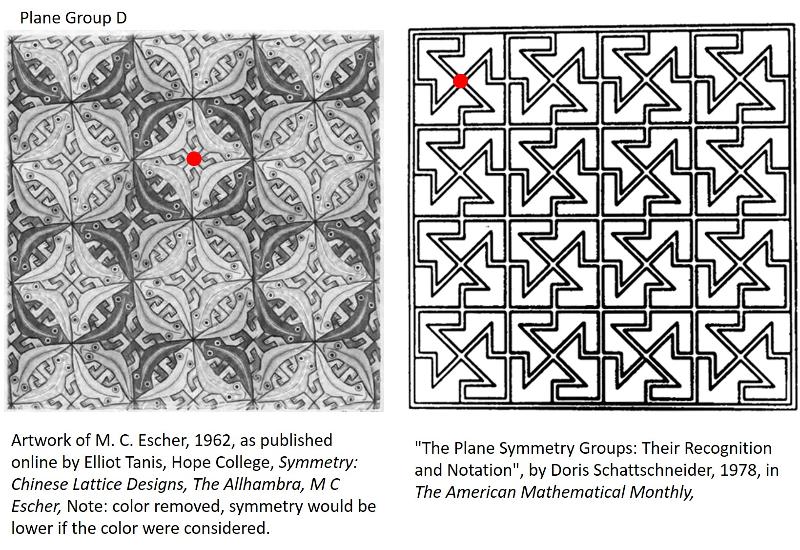
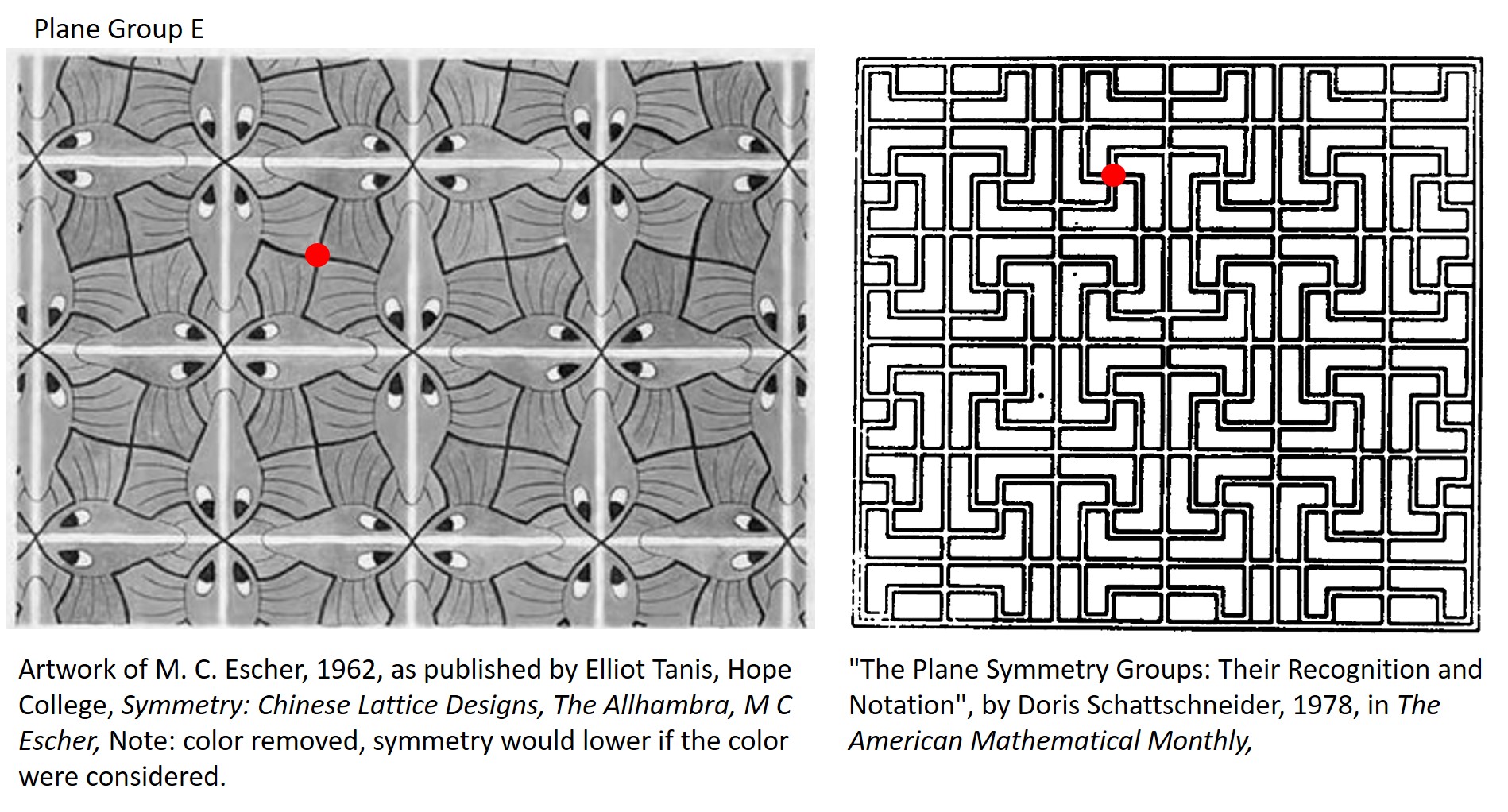
We're going to tackle the Plane Groups in three clusters: 1) The oblique and square systems, 2) the rhombus 6-fold and rhombus 3-fold systems, and 3) the centered rectangle and rectangle systems. For each of the 17 Plane Groups, I will give you two different example patterns to identify. To help you get oriented, I put a small circle at one corner of a reasonable unit cell. Can you identify which Plane Group that each pattern belongs to, based on the symmetries seen in the illustrations above?

 

Examples of Oblique and Square:

Remember, there are two examples of each of the possible plane groups, with a circle on one corner of a reasonable unit cell to help you get oriented. Try to identify the Plane Group for each pair.

 

First, try to sketch out the symmetry elements and unit cell boundaries in the images below.

Plane Group A:

 

Plane Gorup B:

 

Plane Group C:

 

Plane Group D:

 

Plane Group E:

 

 

Examples of Rhombus (6-fold) and Rhombus (3-fold):

Remember, there are two examples of each of the possible plane groups, with a circle on one corner of a reasonable unit cell to help you get oriented. Try to identify the Plane Group for each pair. As a reminder, here are the corresponding plane groups.

 

Plane Groups in the Rhombus System (with maximum 6-fold axis of rotation)

 

Plane Groups in the Rhombus System (with maximum 3-fold axis of rotation)

 

First, try to sketch out the symmetry elements and unit cell boundaries in the images below.

Plane Group F:

 

Plane Group G:

 

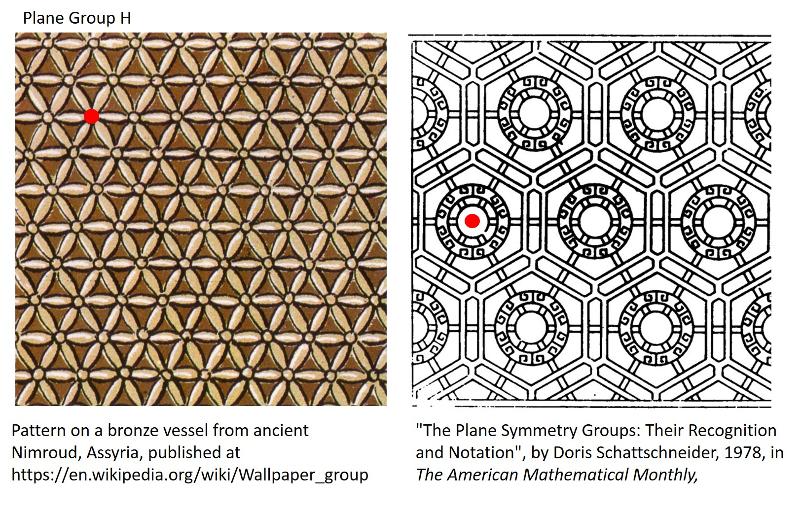
Plane Group H:

 

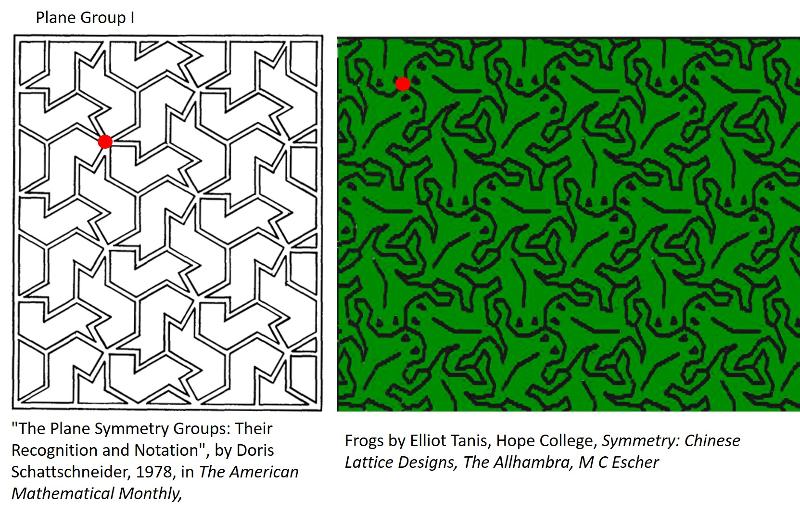
Plane Group I:

 

Plane Group J:

 

 

 

Examples of Centered Rectangle and Rectangle:

Remember, there are two examples of each of the possible plane groups, with a circle on one corner of a reasonable unit cell to help you get oriented. Try to identify the Plane Group for each pair. We have 7 rather than 5 plane groups in this section, plus the differences in the groups can be fairly subtle, so I am providing two additional hints: if there is rotational symmetry in the pattern, it will be shown by the symbol in one corner of the unit cell, and if there is at least 1 glide plane,then at least one glide plane will be shown on the pattern.

As a reminder (the're quite a ways back there!) here are the corresponding plane groups.

 

Plane Groups in the Centered Rectangle System

 

Plane Groups in the Rectangle System

 

First, try to sketch out the symmetry elements and unit cell boundaries in the images below. Glide planes are important in identifying this group, so work at recognizing glide planes. NOtice also that one pattern has a single motif colored in--this can help you recognize the meaning of a motif and understand the difference between a motif and a unit cell.

Plane Group K:

 

 

Plane Group L:

 

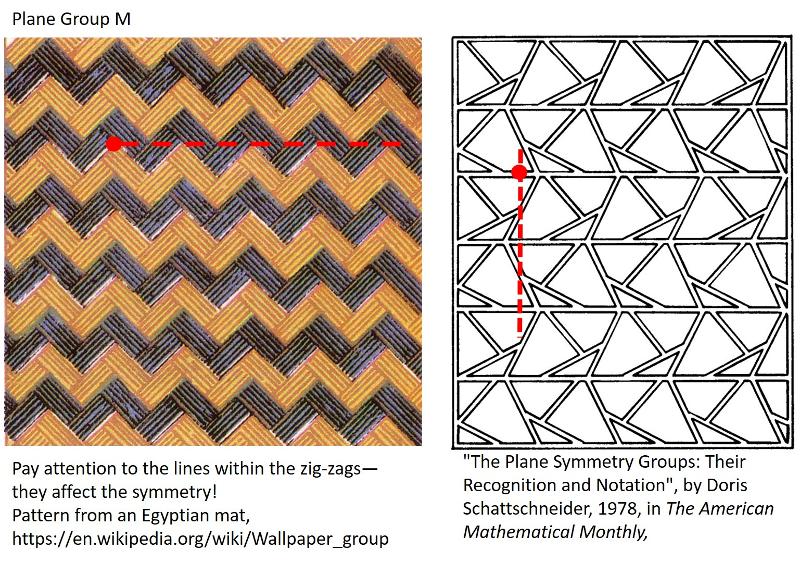
Plane Group M:

 

Plane Group N:

 

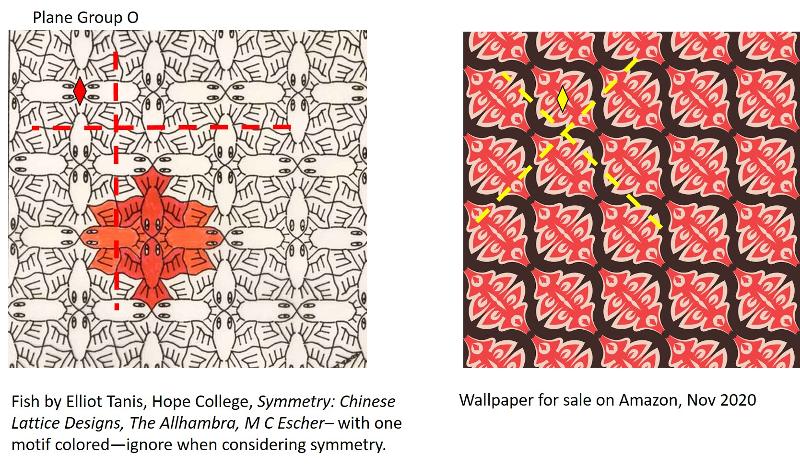
Plane Group O:

 

Plane Group P:

 

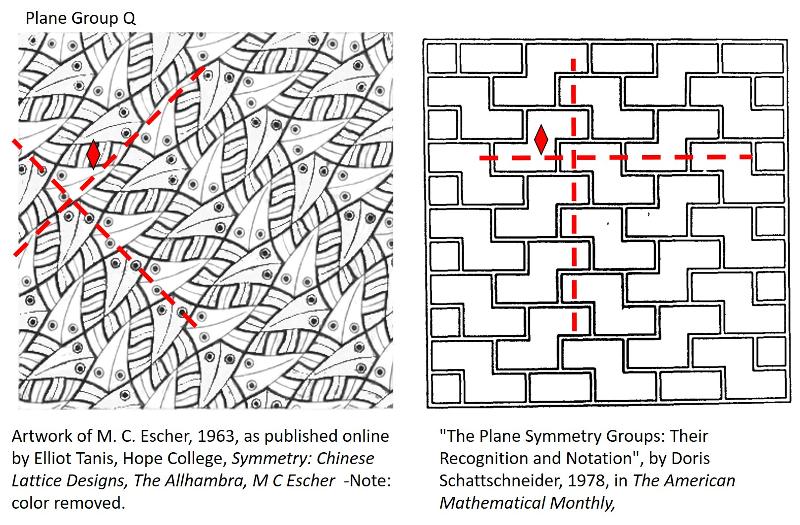
Plane Group Q:

 

 

  

last updated 12/20/2020.   Text and pictures are the property of Russ Colson except where specifically noted. Patterns and illustrations come from a variety of sources including wallpaper for sale on Amazon fall 2020, artwork of M. C. Escher, Symmetry Aspects of M.C. Escher's Periodic Drawings by Caroline MacGillavry (1965), "The Plane Symmetry Groups: Their Recognition and Notation", by Doris Schattschneider, 1978, in The American Mathematical Monthly, https://en.wikipedia.org/wiki/Wallpaper_group (Nov 2020), and http://365daysofpattern.blogspot.com, posting of 2015/06, Other imagery comes from Crystal System at https://en.wikipedia.org/wiki/Crystal_system, and Mineral Science, 23rd edition by Klein and Dutrow.